1515. Повторяющийся Иосиф

По кругу стоят n людей, занумерованных от 1 до n. Начиная отсчет с первого и двигаясь по кругу, будем казнить каждого второго человека до тех пор пока не останется один. Пусть этот выживший имеет номер x. Расставим по кругу x людей и повторим процедуру, после которой выживет человек с номером y. И так далее до тех пор, пока номер выжившего не станет равным первоначальному количеству людей в текущем раунде.

Например, при n = 5 последовательно будут казнены 2, 4, 1, 5. Выживет номер 3. Он не равен 5 (количеству людей в раунде), поэтому следует повторить процедуру. Для n = 3 казнены будут 2, 1. Выживет человек с номером 3, равным n. Процедура заканчивается.

Вход. Состоит из нескольких тестов. Каждый тест в одной строке содержит одно число n (0 < n £ 30000)

Выход. Для каждого теста вывести в отдельной строке его номер как указано в примере, количество повторений процедуры казни после первой итерации и номер выжившего в конце процедуры.

Пример входа	Пример выхода
2 13 23403	Case 1: 2 7 Case 2: 8 1023

РЕШЕНИЕ

рекурсия

Анализ алгоритма

Пусть n – количество людей в круге. Обозначим через f(n) номер последнего уцелевшего. Положим f(1) = 1.

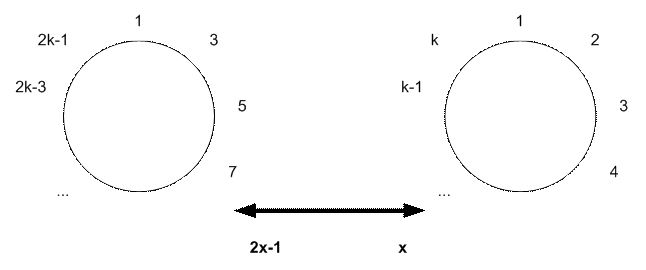
Если n = 2k – четное, то после прохода первого круга будут удалены люди с четными номерами: 2, 4, ..., 2k. Останутся люди с нечетными номерами, а отсчет продолжаем с номера 1. Это все равно, что если бы у нас было k людей, а номер каждого удвоился и уменьшился на 1. То есть получим соотношение f(2k) = 2 f(k) – 1. Например, если в круге из k людей выжившим будет 4-ый, то в исходном круге из 2k людей выжившим будет 2 * 4 – 1 = 7-ой.

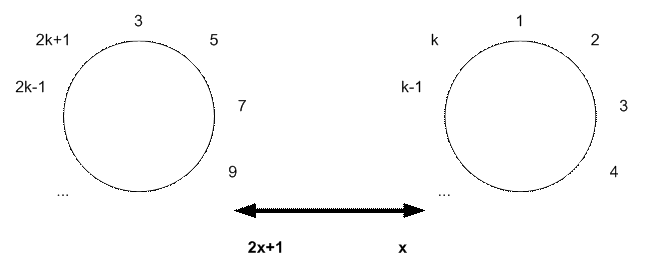
Если n = 2k + 1 – нечетное, то после прохода первого круга будут удалены люди с четными номерами 2, 4, ..., 2k, а жертва с номером 1 уничтожается сразу же после жертвы с номером 2k. Остается k людей с номерами 3, 5, 7, …, 2k + 1. Это все равно, что люди занумерованы от 1 до k, только номер каждого удвоился и увеличился на 1. Получаем соотношение: f(2k + 1) = 2 f(k) + 1.

Объединяя полученные соотношения, получим рекуррентность (1):

f(1) = 1

f(2k) = 2 f(k) – 1, k ³ 1

f(2k + 1) = 2 f(k) + 1, k ³ 1

Составим таблицу первых значений f(n):

Если сгруппировать значения n по степеням 2, то в каждой группе f(n) будет всегда начинаться с 1, а затем увеличиваться на 2. Если записать n в виде n = 2^m + l, где 2^m – наибольшая степень 2, не превосходящая n, а l – то что останется, то решение рекуррентного соотношения должно быть следующим:

f(2^m + l) = 2l + 1, где m ≥ 0, 0 ≤ l < 2^m (2)

Последнее неравенство справедливо, так как l = n – 2^m < 2^m+1 – 2^m = 2^m.

Доказательство последнего соотношения проведем по индукции по m.

База индукции. При m = 0 получим l = 0, откуда f(1) = 1.

Шаг индукции. Имеем m > 0. Индуктивный шаг следует провести как для четного, так и нечетного значения l. Если l четно, то

f(2^m + l) = 2 f(2^m-1 + l / 2) – 1 = 2 (2 l / 2 + 1) – 1 = 2l + 1

Если l нечетно, то

f(2^m + l) = 2 f(2^m-1 + (l – 1) / 2) + 1 = 2 (2 (l – 1) / 2 + 1) + 1 = 2l + 1

Из рекуррентности (1), например, следует соотношение f(2k + 1) – f(2k) = 2.

Пример. f(100) = f(2⁶ + 36) = 2 * 36 + 1 = 73, f(73) = f(2⁶ + 9) = 2 * 9 + 1 = 19.

Теорема. Значение f(n) получается путем циклического сдвига двоичного представления числа n влево на один бит. Например, f(100) = f(1100100₂) = 1001001₂ = 73, f(73) = f(1001001₂) = 10011₂ = 19.

Доказательство. Рассмотрим бинарное представление числа

n = b_mb_m-1…b₁b₀ = 1b_m-1…b₁b₀ (первый бит b_m обязательно равен 1)

Если n = 2^m + l, то l = 0b_m-1…b₁b₀. Тогда 2l + 1 = b_m-1…b₁b₀1. Исходя из равенства f(2^m + l) = 2l + 1, получим

f(1b_m-1…b₁b₀) = b_m-1…b₁b₀1 или f(b_mb_m-1…b₁b₀) = b_m-1…b₁b₀b_m,

что и требовалось доказать.

Многократное применение функции f порождает последовательность убывающих значений, достигающих неподвижной точки n такой что f(n) = n. Число n будет состоять из одних единиц со значением 2^v(n) – 1, где v(n) – количество единиц в бинарном представлении числа n.

Пример

Рассмотрим входные данные для второго теста. При n = 13 последовательно будут казнены 2, 4, 6, 8, 10, 12, 1, 5, 9, 13, 7, 3. Выживет номер 11. Он не равен 13 (количеству людей в раунде), поэтому следует повторить процедуру. Для n = 11 казнены будут 2, 4, 6, 8, 10, 1, 5, 9, 3, 11. Выживет человек с номером 7, равным n. При n = 7 выживет номер 7. После первой итерации проведено еще 2 повторения процедуры казни.

f(13) = f(1101₂) = 1011₂ = 11, f(11) = f(1011₂) = 111₂ = 7, f(7) = 7.

Реализация алгоритма

Функция last по первоначальному количеству людей n в круге возвращает номер уцелевшего согласно рекуррентному соотношению.

int last(int n)

{

if (n == 1) return 1;

if (n % 2 == 0)

return 2 * last(n / 2) - 1;

else

return 2 * last((n - 1) / 2) + 1;

}

Переменная r содержит количество повторений процедуры казни (изначально r = 0). По заданному входному n ищем номер уцелевшего k. Если он не равен n, то повторяем в цикле процедуру казни.

scanf("%d",&tests);

for(i = 1; i <= tests; i++)

{

scanf("%d",&n); r = 0;

while ((k = last(n)) != n) r++, n = k;

printf("Case %d: %d %d\n",i,r,n);

}