1518. Разбиение треугольника

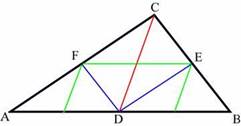
Треугольник можно разбить на два треугольника, проведя медиану к его большей стороне (на рисунке сверху такое разбиение показано красным разрезом). Затем два меньших треугольника можно подобным образом разделить на четыре треугольника (на рисунке такое разбиение показано синими разрезами). Процесс разрезания треугольников будем продолжать до бесконечности.

Математики заметили, что при описанном разрезании мы получим конечное количество "стилей" треугольников, которые отличаются друг от друга только размером. По заданным длинам сторон исходного треугольника необходимо определить количество стилей треугольников, которое можно получить. Два треугольника принадлежат одному стилю, если они подобны.

Вход. Первая строка содержит количество тестов n (0 < n < 35). Каждая следующая строка содержит три целых числа a, b, c (0 < a, b, c < 100) – стороны треугольника. Известно, что площадь каждого входного треугольника положительна.

Выход. Для каждого теста в отдельной строке вывести его номер, как показано в примере, и целое число t – количество разных стилей треугольников, которое получится в процессе указанного деления. Считать, что значение t всегда меньше 100.

Пример входа	Пример выхода
2 3 4 5 12 84 90	Triangle 1: 3 Triangle 2: 41

РЕШЕНИЕ

рекурсия - геометрия

Анализ алгоритма

Два треугольника считаются подобными (принадлежат одному стилю), если отношения их сторон одинаковы. Стилем треугольника со сторонами a, b, c (a ≤ b ≤ c) будем называть пару (b / a, c / a). Тогда два треугольника будут подобными, если их стили одинаковы.

Промоделируем процесс разрезания треугольников медианами, запоминая их стили. Если на очередном шаге получим треугольник уже имеющегося стиля, то дальше его разрезать не будем. Поскольку по условию задачи стилей не больше 100, то и число разрезаний будет удовлетворять этому условию.

Для каждого треугольника отсортируем длины его сторон: a ≤ b ≤ c. То есть самой длинной стороной бедет с. Длина медианы, проведенной к ней, равна

Таким образом, треугольник со сторонами (a, b, c) будет разрезан на два треугольника со сторонами (a, m, c/2) и (b, m, c/2).

Реализация алгоритма

Стиль i-го треугольника будем запоминать в паре (y[i], z[i]). В переменной ptr будем подсчитывать количество стилей.

double y[101],z[101];

int ptr;

Добавление треугольника со сторонами (x₁, y₁, z₁) в базу стилей. Если его стиль уже встречался ранее, то ничего не делаем. Иначе заносим пару (y₁ / x₁, z₁ / x₁) в (y[ptr], z[ptr]) и увеличиваем ptr на 1.

int add(double x1, double y1, double z1)

{

y1 = y1 / x1; z1 = z1 / x1;

for(int i = 0; i < ptr; i++)

if ((fabs(y1 - y[i]) < 0.000001) && (fabs(z1 - z[i]) < 0.000001))

return 0;

y[ptr] = y1; z[ptr] = z1;

return ++ptr;

}

Разбиваем треугольник со сторонами (a, b, c) на два со сторонами (a, m, c/2) и (b, m, c/2). Перед разбиением сортируем стороны в неубывающем порядке. Рекурсивно запускаем разбиение полученных треугольников.

void triangle(double a, double b, double c)

{

double temp[3] = {a,b,c};

sort(temp,temp+3);

if(!add(temp[0],temp[1],temp[2])) return;

double m = sqrt(2*temp[0]*temp[0] + 2*temp[1]*temp[1] –

temp[2]*temp[2]) / 2;

triangle(temp[0],m,temp[2]/2);

triangle(temp[1],m,temp[2]/2);

}

Основная часть программы.

scanf("%d",&n);

for(test = 1; test <= n; test++)

{

scanf("%lf %lf %lf",&a,&b,&c);

ptr = 0; triangle(a,b,c);

printf("Triangle %d: %d\n",test,ptr);

}