1521. Optimal matrix multiplication
– 2
Given two matrices A and B, we can determine the
matrix C = AB using the standard definition of matrix
multiplication:
![]()
The number of columns in the matrix A must be the same as the number of
rows in the matrix B. Let matrix A has size m
× n, matrix B has size n × p. Then matrix С wil have the size m × p, and to calculate it you should perform m * n * p multiplications.

For example, if size of A is 10 × 20, size of B is 20 × 15,
it will take 10 × 20 × 15 = 3000 multiplications to compute
matrix C.
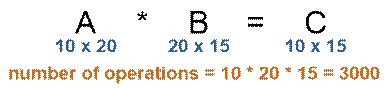
Multiplication of more than two matrices can be done in multiple ways.
For example, if X, Y and Z are matrices, then XYZ computation can be done
either like (XY)Z or X(YZ). Let size of X be
5 × 10, size of Y be 10 × 20, and size of Z be 20
× 35.

Let's look at the number of multiplications required to compute the
product using two different ways:
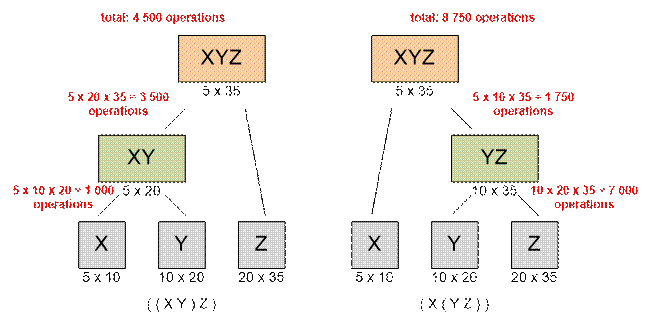
(XY)Z
·
5 × 10 × 20 =
1000 multiplications to determine the product (XY) that has size 5 × 20.
·
Then 5 × 20 × 35
= 3500 multiplications to find the final result.
·
Total number of
multiplications: 4500.
X(YZ)
·
10 × 20 × 35 =
7000 multiplications to determine the product (YZ) that has size 10 × 35.
·
Then 5 × 10 × 35
= 1750 multiplications to find the final result.
·
Total number of
multiplications: 8750.
Clearly we'll be able to compute (XY)Z using fewer multiplications.
Given the sequence of matrices to be multiplied, you are to determine
the optimal order of their multiplication. Optimality in this problem is
relative to the number of scalar multiplications required.
Input. Consists of multiple test cases. The first line of each test case
contains the number n (n ≤ 10) of matrices to be
multiplied. It is followed by n pairs
of integers, each pair giving the number of rows and columns in a matrix,
matrix sizes are given in the order of their multiplication. The last test case
contains n = 0 and should
not be processed.
Output. Assume that matrices are named A1, A2,..., An. Your output for each input case must
be a line containing a parenthesized expression clearly indicating the order in
which the matrices should be multiplied. Prefix the output for each case with
the case number (they are sequentially numbered, starting with 1). Your
output must strongly resemble the samples shown below. If, by chance, there are
multiple correct sequences, any of these will be accepted as a valid answer.
|
Sample input |
Sample output |
|
3 1 5 5 20 20 1 3 5 10 10 20 20 35 6 30 35 35 15 15 5 5 10 10 20 20 25 0 |
Case 1:
(A1 x (A2 x A3)) Case 2:
((A1 x A2) x A3) Case 3:
((A1 x (A2 x A3)) x ((A4 x A5) x A6)) |
SOLUTION
dynamic programming
Анализ алгоритма
Обозначим через Aij
произведение матриц Ai * Ai+1 *
… * Aj-1 * Aj (1 £ i £ j £ n), через m[i, j] минимальное
количество умножений, необходимое для вычисления Aij. Стоимость
вычисления всего произведения A1n будет храниться в m[1, n].
Значения m[i, i] = 0, поскольку Aii = Ai
и для его нахождения вычисления не нужны.
Количество столбцов матрицы Ai
равно количеству строк матрицы Ai+1. Это значение
хранится в p[i]. Количество строк матрицы А1 находится в
p[0], а количество столбцов An – в p[n].
Предположим, что при оптимальной
расстановке скобок в произведении Ai * … * Aj
последней операцией умножения будет (Ai * … * Ak
) * (Ak+1
* … * Aj). Значение m[i, j] равно сумме
минимальной стоимости вычислений Aik и Ak+1j
плюс стоимость умножения этих двух матриц:
m[i, j] = m[i, k]
+ m[k + 1, j] + p[i – 1] * p[k] * p[j]
При этом число k может
принимать только j – i разных значений: i, i + 1,
…, j – 1. Поскольку только одно из них является оптимальным, то
необходимо перебрать все эти значения и выбрать наилучшее. Получим рекуррентную
формулу:
m[i, j] = 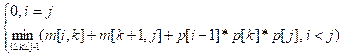
Для запоминания оптимального
умножения положим s[i, j] = k, если при оптимальном
вычислении Ai * … * Aj последней операцией
будет умножение Ai * … * Ak на Ak+1
* … * Aj.
Пример
Рассмотрим
третий тест. Данные о размерах входных матриц сохраняются в массиве p:
![]()
Минимальная стоимость вычисления
матриц Aij хранится в ячейках массива m[i, j]:
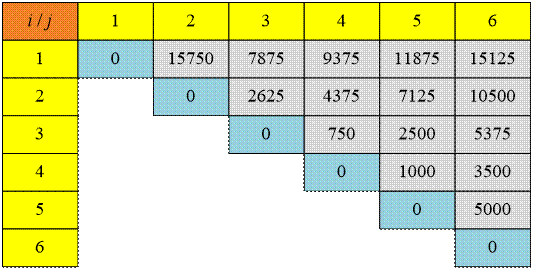
Соответствующие
значения матрицы s:
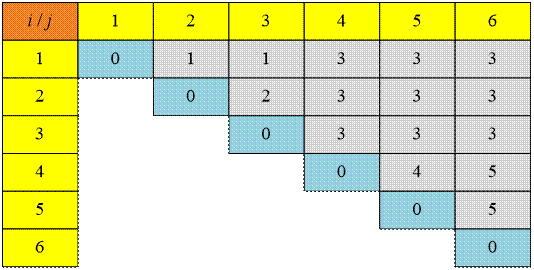
Для
умножения шести входных матриц достаточно выполнить m[1,6] = 15125
операций умножения. Оптимальная
последовательность умножений имеет вид:
A16
= (s[1,6] = 3) = A13 * A46 =
(s[1,3] =
1, s[4,6] = 5) = (A11 * A23) * (A45 * A66)
=
(s[2,3] =
2, s[4,5] = 4) = (A11 * (A22 * A33 ) ) * ((A44
* A55) * A66) =
(A1
* (A2 * A3 ) ) * ((A4 * A5) * A6)
Реализация алгоритма
Let
INF =
∞, MAX is
the maximum possible number of matrices in the product. Объявим строковый массив Stroka, в
котором храним числа от 0 до 10 в виде строк. Объявим массивы m, s, p, описанные
выше. В переменной Answer будем накапливать результат.
#define INF 0x3F3F3F3F3F3F3F3F
#define MAX 11
string Stroka[11] = {"0","1","2","3","4","5","6","7","8","9","10"};
long long m[MAX][MAX], s[MAX][MAX], p[MAX];
string
Answer;
Функция Mult находит минимальное
количество умножений, необходимое для вычисления Aij = Ai
* Ai+1 * … * Aj-1 * Aj,
которое сохраняем в ячейке m[i, j].
long long
Mult(int i, int
j)
{
if (m[i][j] == INF)
for (int k = i; k
<= j - 1; k++)
{
long long temp =
Mult(i,k) + Mult(k+1,j) + p[i-1] * p[k] * p[j];
if (temp < m[i][j])
{
m[i][j] = temp;
s[i][j] = k;
}
}
return m[i][j];
}
Функция Print(i, j)
выводит оптимальное произведение матриц Ai * Ai+1
* … * Aj-1 * Aj согласно формату
вывода.
string Print(int i, int j)
{
if (i == j) return "A" + Stroka[i];
return "("
+ Print(i,s[i][j]) + " x " +
Print(s[i][j]+1,j) + ")";
}
Основной цикл программы. Переменная cs содержит
номер теста.
cs = 1;
while(scanf("%d",&n),n)
{
Присвоим всем ячейкам массива m значения «бесконечность».
memset(m,0x3F,sizeof(m));
Читаем размеры входных матриц,
сохраняем их в массиве p. Положим m[i, i] = 0.
for(i = 1; i <= n; i++)
{
scanf("%d %d",&p[i-1],&p[i]); m[i][i] =
0;
}
Вычисляем результат – ищем
оптимальное произведение матриц A1 * A2 * … * An-1
* An.
Mult(1,n);
Выводим номер теста cs. Если n = 1, то
перемножать нечего и следует вывести строку "(A1)". Иначе вызываем
функцию Print(1,n), которая возвращает строку, содержащую
последовательность оптимального произведения матриц.
printf("Case %d: ",cs++);
if (n == 1)
Answer = "(A1)"; else Answer = Print(1,n);
Выводим результат – строку Answer.
printf("%s\n",Answer.c_str());
}