1523. Трамваи в Барселоне
Недавно в
Барселоне трамвай включили в "эффективную" транспортную систему
города. Как и ожидалось, результатом такого решения стало появление поломок,
отличавшихся оригинальностью и красотой. Но не смотря на такую эстетику, мер Барселоны
решил уменьшить время заторов, которые возникали в результате аварий. После скрупулезного
изучения проблемы, он огласил следующую модель движения:
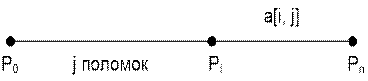
Каждый трамвай
должен проехать с начальной станции P0 до конечной Pn, посетив промежуточные
станции P1, ..., Pn – 1 именно в таком
порядке. Для каждого 1 ≤ i
≤ n, пусть Si – длина пути (секции) от Pi – 1 до Pi. Каждая такая секция должна
быть пройдена с постоянной скоростью vi,
которая выбирается водителем на станции Pi-1.
Пусть Mi – максимальная
возможная скорость трамвая на участке Si,
и пусть выбранная на нем скорость равна 0 < vi ≤ Mi.
Вероятность поломки на участке Si
равна vi / Mi. В случае аварии у трамвая
включается система восстановления, на что уходит всего 10 секунд. Затем трамвай
едет до Pi, используя
дополнительный (медленный, но безопасный) двигатель, со скоростью 5 метров в
секунду, и уже без поломок на Si.
Например, пусть
длина секции равна 300 метров, а максимально возможная скорость на этом участке
равна 25 метров в секунду. Если водитель выберет скорость 25 м/с, то трамвай
однозначно сломается. Так как авария может произойти где угодно между Pi-1 и Pi, то для удобства будем
считать, что она произойдет как раз в середине пути (после 150 метров). Таким
образом, трамвай проедет 6 секунд до середины пути, 10 секунд постоит пока
будет включаться дополнительный двигатель после поломки, и за 30 секунд он
достигнет Pi, всего таким
образом потратив на путь 46 секунд. Если начальная скорость трамвая будет 15
м/с, то с вероятностью 0.6 он сломается и доедет за 10 + 10 + 30 = 50 секунд, и
с вероятностью 0.4 достигнет Pi
через 20 секунд без поломки. Среднее время проезда в этом случае составит
0.6·50 + 0.4·20 = 38 секунд.
Когда трамвай
достигает Pi, он
останавливается на несколько секунд независимо от того была авария на Si или нет; этих нескольких
секунд (для простоты вычислений будем считать их равными 0) достаточно чтобы
полностью отремонтировать трамвай: максимальная возможная скорость уменьшается
на 1 м/с после каждой поломки. Если начальная возможная максимальная скорость
равна M0, то Mi
= M0 – Ci, где
0 ≤ Ci ≤ i – 1 общее количество аварий на
участках S1, ..., Si-1.
Напишите
программу, которая выведет наименьшее среднее время путешествия, если известна
начальная максимальная допустимая скорость движения трамвая и длина каждой
секции.
Вход. Каждая строка
соответствует одному тесту и содержит начальную максимально возможную скорость
трамвая M0 (действительное число между 5 и 25), значение n (целое число между 1 и M0 –
1), и длины всех секций (действительное число от 100 до 1000).
Выход. Для каждого теста в отдельной строке вывести минимальное
среднее время, за которое трамвай преодолеет весь путь. Ответ следует выводить
с четырьмя десятичными знаками.
|
Пример входа |
Пример выхода |
|
25 1 900 25 2 900 900 25 2 305.15 980.76 5 1 1000 |
102.0000 205.0303 150.0000 210.0000 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
f(x) = ![]()
![]() +
+ ![]()
![]()

Найдем скорость x, для которой это время
минимально. Раскроим скобки и сгруппируем:
f(x) = ![]() + x
+ x ![]() –
– ![]()
Производная равна
f’(x) = ![]() +
+ ![]() =
= ![]()
Приравняем ее к нулю, и решим уравнение относительно x: ![]() . Получим оптимальную скорость
. Получим оптимальную скорость
x = ![]()
Пусть a[i,
j] – минимальное время, за которое можно доехать с остановки Pi
до конца маршрута при условии, что до этого было j поломок. Очевидно,
что a[n, i] = 0.
Обозначим через:
T0 = a[i
+ 1, j] – оптимальное время, за которое можно доехать с Pi+1
до конца с j поломками,
T1 = a[i
+ 1, j + 1] – оптимальное время, за которое можно доехать с Pi+1
до конца с j + 1 поломками.
Тогда среднее время проезда от Pi до
конца равно
f(x) = ![]()
![]() +
+ ![]()
![]()
Приравниваем производную к нулю (решаем уравнение f’(x) = 0), вычисляем скорость x, для которой это время будет
минимальным. Она равна
x = 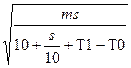
При вычислении a[i,
j] следует помнить, что до Pi было j поломок. Тогда
максимально возможная скорость, которую трамвай может выбрать на Si+1,
равна m = M0 – j. Если вычисленная оптимальная
скорость x будет больше чем M0 – j, то положить x
= M0 – j.
Оптимальное среднее время, за которое трамвай проедет весь
путь, равно a[0, 0]. Вычисление
значений массива a идет с конца
(сначала вычисляется столбик a[n
– 1, i] (0 £ i £ n – 1), потом a[n
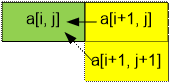
– 2, i] (0 £ i £ n – 2) и так далее до a[0, 0]). Каждое значение a[i,
j] пересчитывается через a[i
+ 1, j] и a[i + 1, j
+ 1].
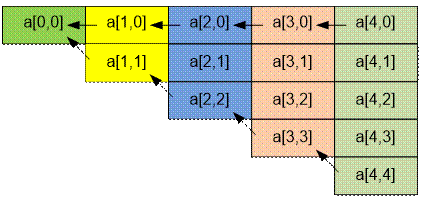
Пример
Рассмотрим второй тест. Данные матрицы a вместе с оптимальными значениями
скоростей x приведены в таблице:
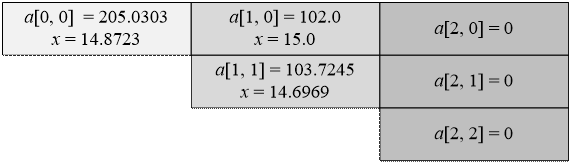
Вычислим a[1, 1]. Оптимальная
скорость равна:
x = 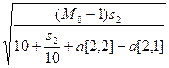 =
=  =
= ![]() =
= ![]() ≈ 14.6969
≈ 14.6969
a[1, 1] = ![]()
![]() +
+ 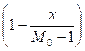
![]() ≈ 103.7245
≈ 103.7245
Вычислим a[1, 0]. Оптимальная скорость
равна:
x = 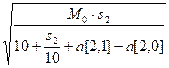 =
= 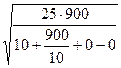 =
= ![]() = 15
= 15
a[1, 0] = ![]()
![]() +
+ 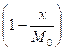
![]() = 102
= 102
Вычислим a[0, 0]. Оптимальная
скорость равна:
x = 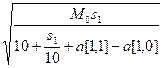 =
= 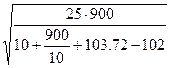 =
= ![]() ≈ 14.8723
≈ 14.8723
a[0, 0] = ![]()
![]() +
+ 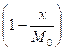
![]() ≈ 205.0303
≈ 205.0303
Реализация
алгоритма
Читаем входные данные и обнуляем последний столбец матрицы
a (a[n, i] = 0, 0 £ i £ n).
while(scanf("%lf %d",&m0,&n) == 2)
{
for(i = 0; i < n; i++) scanf("%lf",&s[i]);
for(i = 0; i
<= n; i++) a[n][i] = 0;
Динамически пересчитываем значения i - го столбца
через (i + 1) - ый (0 £ i £ n – 1). Данные
каждого столбца вычисляем сверху вниз, двигаясь от a[i, 0] до a[i,
i].
for(i = n - 1; i >= 0; i--)
for(j = 0; j <= i; j++)
{
x = sqrt((m0-j) * s[i] /
(10
+ s[i]/10 + a[i+1][j+1] - a[i+1][j]));
if (x > m0 - j) x = m0 - j;
a[i][j] = (x / (m0 - j))
* (s[i]/2/x + 10 + s[i]/10 +
a[i+1][j+1])
+ (1 - x/(m0-j)) * (s[i]/x + a[i+1][j]);
}
Выводим результат с 4 десятичными знаками после запятой.
printf("%.4lf\n",a[0][0]);
}