1524. Распределение оценок
В
экзаменационный период студент сдал n
предметов, за которые в сумме получил t
баллов. Наименьший балл, при котором ставится зачет по каждому предмету, равен p. Вам следует подсчитать количество
способов, которыми студент мог получить баллы на экзаменах. Например, если n = 3, t = 34 и p = 10, то баллы
по трем предметам могли распределиться следующими способами:
|
|
Предмет 1 |
Предмет 2 |
Предмет 3 |
|
1 |
14 |
10 |
10 |
|
2 |
13 |
11 |
10 |
|
3 |
13 |
10 |
11 |
|
4 |
12 |
11 |
11 |
|
5 |
12 |
10 |
12 |
|
6 |
11 |
11 |
12 |
|
7 |
11 |
10 |
13 |
|
8 |
10 |
11 |
13 |
|
9 |
10 |
10 |
14 |
|
10 |
11 |
12 |
11 |
|
11 |
10 |
12 |
12 |
|
12 |
12 |
12 |
10 |
|
13 |
10 |
13 |
11 |
|
14 |
11 |
13 |
10 |
|
15 |
10 |
14 |
10 |
Студент может
сдать сессию 15 способами.
Вход. Первая строка содержит количество тестов. Каждый тест
содержит в одной строке три числа n, t и p,
значения каждого из которых не больше 70.
Выход. Для каждого
теста вывести количество способов, которыми студент может сдать экзамен. Ответ
всегда является знаковым 32-битовым
целым числом.
|
Пример
входа |
Пример
выхода |
|
2 3 34 10 3 34 10 |
15 15 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Количество
способов, которыми студент может сдать экзамен, равно количеству разложений
числа t – n*p на n неотрицательных слагаемых.
Обозначим через
f(n, k) количество разбиений числа n на k
неотрицательных слагаемых. Если при разбиении числа n на k
неотрицательных слагаемых последнее (k - ое) слагаемое равно i (0
£ i £ n), то
далее число n – i следует разбить на k – 1 слагаемых, что
можно совершить f(n – i, k – 1) способами. Поскольку 0 £ i £ n, то
общее число разбиений f(n, k) равно f(n, k – 1) +
f(n – 1, k – 1) + f(n – 2, k – 1) + … f(1, k –
1) + f(0, k – 1). Или то же самое что
f(n, k)
= ![]()
Очевидно, что f(n,
1) = 1, так как количество способов
разбить число n на одно слагаемое равно единице (этим слагаемым будет
само число n). Имеет место соотношение f(0, k) = 1, так как
единственным разложением числа 0 на k слагаемых будет 0 = 0 + 0 + … + 0
(k раз). Заведем массив m, в котором положим m[k, n] = f(n,
k), 1 £ k, n £ 100. Индексы массива m и функции f переставлены для удобства
программирования: очередная k - ая строка массива m пересчитывается
через предыдущую (k – 1) - ую строку. Временная оценка алгоритма O(n2).

Заметим, что
f(n, k)
= f(n, k – 1) + ( f(n – 1, k – 1) + f(n – 2,
k – 1) + … f(1, k – 1) + f(0, k – 1) ) =
= f(n, k
– 1) + f(n – 1, k)
То есть m[k, n] = m[k, n – 1] + m[k – 1, n]:
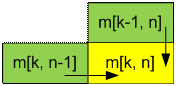
Задача имеет
также комбинаторное решение через сочетания с повторениями. Если f(n, k)
равно количеству разбиений числа n на k неотрицательных
слагаемых, то
f(n, k)
= ![]() =
= ![]()
Пример
Для n =
20 и k = 2 существует 21 разбиение: 0 + 20, 1 + 19, 2 + 18, ..., 19 + 1,
20 + 0.
Для начальных
значений n, k таблица m[k, n] имеет вид:
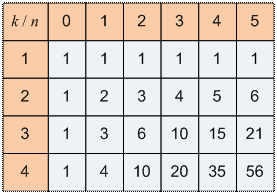
По формуле
сочетаний с повторениями имеем: f(20, 2) = ![]() =
= ![]() = 21.
= 21.
Рассмотрим тест n = 4, t = 21 и p = 2.
Необходимо найти количество разложений числа t – n*p = 21 – 4 * 2 = 13 на 4 неотрицательных
слагаемых. Оно равно
f(13, 4) = ![]() =
= ![]() =
= ![]() = 560
= 560
Реализация алгоритма
Определим размер
MAX массива m и объявим сам массив m.
#define MAX 71
int m[MAX][MAX];
Обнуляем массив
m. Проведем инициализацию, положив f(i, 1) = f(0, i) = 1 (0 £ i < MAX). Значения m[i, j]
пересчитываем как сумму m[i, j – 1] и m[i – 1, j]. Находим значения
всех ячеек массива m, совершая таким образом предвычисления.
memset(m,0,sizeof(m));
for(i = 0; i < MAX; i++) m[1][i] =
m[i][0] = 1;
for(i = 2; i < MAX; i++)
for(j = 1; j
< MAX; j++)
m[i][j] = m[i][j-1] + m[i-1][j];
Читаем
количество тестов tests. Для каждого
теста вводим значения n, t, p.
Положим t = t – n * p. Выводим результат, хранящийся в
ячейке m[n, t].
scanf("%d",&tests);
while(tests--)
{
scanf("%d %d
%d",&n,&t,&p);
t -= n * p;
printf("%d\n",m[n][t]);
}