1525. A Grouping Problem

You are given a set of n integers. You may choose k distinct elements from this set to form a group. Two groups are considered different if there exists at least one element that is present in one group but not in the other. For example, if the set contains 4 elements a, b, c, d, and you are asked to choose two elements, then ab, ac, ad, bc, bd and cd are all valid and distinct groups.

A grouping system is called complete if, for a given k, the number of different groups is maximized. In this example, the set {ab, ac, ad, bc, bd, cd} forms a complete grouping system.

For a particular complete grouping system, the fitness is computed as follows:

· Each group contributes the product of all numbers in that group;

· All group contributions are summed;

· The fitness is defined as the total contribution mod m, where m is the bounding parameter.

In the example above, for k = 2, the fitness is

F₂ = (ab + ac + ad + bc + bd + cd) mod m

If k = 1, the fitness is

F₁ = (a + b + c + d) mod m

Your task is to determine the complete grouping system that yields the maximum possible fitness.

Input. Each test case starts with two positive integer n (2 ≤ n ≤ 1000) and m (1 ≤ m < 2³¹). The next line contains n positive integers, each at most 1000. The input terminates with a case where n = m = 0.

Output. For each test case, print a single line containing the maximum possible fitness for a grouping system.

Sample input	Sample output
4 10 1 2 3 4 4 100 1 2 3 4 4 6 1 2 3 4 0 0	5 50 5

SOLUTION

dynamic programming

Algorithm analysis

Let а₁, a₂, …, a_n be a given set of n integers. Denote by F_ik (i ³ k) the sum of all possible products of k integers chosen from the first i integers a₁, …, a_i. Let us construct the following table of F_ik values:

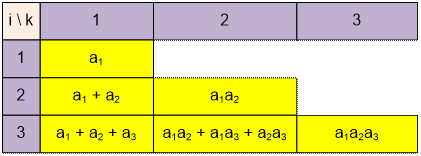
For four numbers, we obtain:

· F_4,1 = a₁ + a₂ + a₃ + a₄;

· F_4,2 = a₁a₂ + a₁a₃ + a₁a₄ + a₂a₃ + a₂a₄ + a₃a₄;

· F_4,3 = a₁a₂a₃ + a₁a₂a₄ + a₁a₃a₄ + a₂a₃a₄;

· F_4,4 = a₁a₂a₃a₄;

The following recurrence relations hold:

F_i1 = F_(i-1)1 + a_i,

F_ii = F_{(i-1) (i-1)} * a_i, 1 £ i £ n

F_ik = F_(i-1)k + F_{(i-1) (k-1)} * a_i, 1 £ i £ n, 1 < k < i

For example,

· F_3,2 = F_2,2 + F_2,1 * a₃ = a₁a₂ + (a₁ + a₂) * a₃ = a₁a₂ + a₁a₃ + a₂a₃;

· F_4,3 = F_3,3 + F_3,2 * a₄ = a₁a₂a₃ + (a₁a₂ + a₁a₃ + a₂a₃) * a₄ =

a₁a₂a₃ + a₁a₂a₄ + a₁a₃a₄ + a₂a₃a₄

The values of each subsequent row are computed based on the values of the previous row, so it is sufficient to store a single linear array d of size up to 1000. The recalculation of the -th row should be performed from the end: first compute F_ii, then F_i(i-1), and so on down to F_i1. All computations must be performed modulo m.

Example

Consider the first test case. We’ll construct two tables: in the first table, computations are performed without the modulo, and in the second table, computations are performed modulo m = 10.

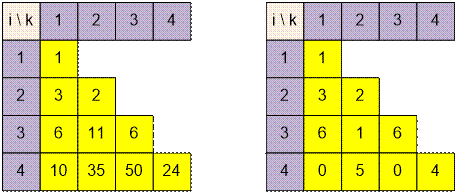
For example,

· F_4,2 = F_3,2 + F_3,1 * 4 = 11 + 6 * 4 = 35;

· F_4,3 = F_3,3 + F_3,2 * 4 = 6 + 11 * 4 = 50;

The answer is the maximum value in the fourth row of the second table.

Algorithm implementation

Declare a linear array d, where the values of F_ik will be recomputed.

long long d[1000];

Read the number of elements n and the value m. For each input test case, the array d is initially cleared. The first number a₁ is stored in d[0].

while (scanf("%lld %lld",&n,&m), n + m > 0)

{

memset(d,0,sizeof(d));

scanf("%lld",&d[0]);

Next, read the value x = a_i+1 (1 £ i < n) and recalculate the values of F_ik for k = i, i – 1, …, 1 using the recurrence formulas given above. All computations are performed modulo m.

for (i = 1; i < n; i++)

{

scanf("%lld",&x);

d[i] = (d[i-1] * x) % m;

for (j = i - 1; j > 0; j--)

d[j] = (d[j-1] * x + d[j]) % m;

d[0] = (d[0] + x) % m;

}

Find the maximum value among the elements of the array d and store it in the variable res.

res = 0;

for (i = 0; i < n; i++)

if (d[i] > res) res = d[i];

Print the answer.

printf("%lld\n",res);

}