1530. Расширенное счастливое число

Дано натуральное число n. Возведем в k - ую степень каждую его цифру и просуммируем полученные результаты. Обозначим результат через S_k(n). Например, S₂(65) = 6² + 5² = 61. Построим последовательность n, S_k(n), S_k(S_k(n)), … .

Счастьем числа n по отношению к k будем называть наименьшее число в этой последовательности.

Вход. Каждая строка является отдельным тестом и содержит три целых числа a, b (1 ≤ a, b ≤ 10⁶) и k (1 ≤ k ≤ 6).

Выход. Для каждого теста вычислить счастье каждого числа от a до b включительно по отношению к k и вывести их сумму.

Пример входа	Пример выхода
13 13 2 1 5 2 535 538 3	1 14 820

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Поскольку значение k в процессе вычислений фиксировано, заведем массив powk, в котором powk[i] = i^k. Им будет удобно пользоваться при вычислении значений S_k(n) в функции sum(n). Наибольшее значение, которое могут принимать элементы последовательности n, S_k(n), S_k(S_k(n)), …, не больше 4*10⁶, так как даже при k = 6 значение S₆(n) при n < 4*10⁶ не больше 3⁶ + 6*9⁶ = 3189375 < 4*10⁶.

Наивное решение задачи состоит в том, чтобы для каждого значения i (a ≤ i ≤ b) строить последовательность i, S_k(i), S_k(S_k(i)), … до тех пор, пока некоторое число не повторится в ней дважды. После этого в последовательности уже не будут появляться новые числа (числа будут повторяться). Остается найти наименьшее значение среди построенных чисел. Однако такое решение работает достаточно долго.

Заведем массив f[4000000], в котором будем хранить f[i] = S_k(i). Рассмотрим для некоторого i последовательность a₀ = i, a₁ = S_k(i), a₂ = S_k(S_k(n)), … . Очевидно, что найдутся такие индексы s и t (пусть s < t для определенности), что a_s = a_t.

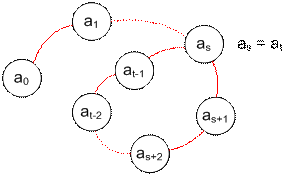
Теперь значение f[a_k], (0 £ k £ t) положим равным минимуму среди чисел a_k, a_k+1, …, a_t. При этом начиная вычислять значение f[a₀], в процессе мы находим все значения f[a_k], 0 £ k £ t.

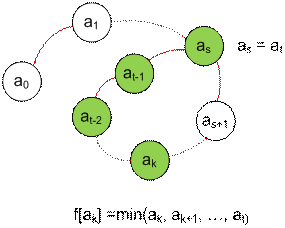
Описанную процедуру совершаем в функции g. Значение f[i] считается вычисленным, если f[i] > 0. При первом проходе по числам a₀, …, a_t устанавливаем f[a_i] = -1. Дойдя до a_t = a_s, продолжаем путь a_s , a_s+1, …, a_t, устанавливая f[a_i] = a_i для s £ i £ t. Когда вторично дойдем до f[a_t], значение этой ячейки уже будет положительным и рекурсия начнет раскручиваться назад. Двигаясь назад по кольцу дважды от a_t до a_s, а потом и до a₀, устанавливаем f[a_i] в наименьшее значение среди чисел a_i, a_i+1, …, a_t.

Реализация алгоритма

Объявим необходимые массивы и переменные.

#define MAX 5000001

int powk[10], f[MAX], ptr;

long long res;

Функция sum вычисляет значение S_k(n), равное сумме k - ых степеней всех его цифр.

int sum(int n)

{

int s;

for(s = 0; n; n /= 10)

s += powk[n % 10];

return s;

}

int g(int n)

{

Если значение f[n] уже вычислено, то возвращаем его.

if (f[n] > 0) return f[n]; else

При первом проходе по числам a₀, …, a_s, …, a_t = a_s устанавливаем f[a_i] = -1.

if (f[n] == 0) f[n] = -1; else

Сюда попадаем, когда дойдем до a_s второй раз (часть пути от a₀ до a_s и полный круг от a_s до a_s).

if (f[n] == -1) f[n] = n;

return f[n] = min(n,g(sum(n)));

}

Функция calcTheSum вычисляет сумму счастья всех чисел от a до b включительно по отношению к k.

long long calcTheSum(int a, int b, int k)

{

int i, j, s;

long long res = 0;

for(i = 0; i < 10; i++)

{

for(s = 1, j = 0; j < k; j++) s *= i;

powk[i] = s;

}

for(i = a; i <= b; i++)

res += g(i);

return res;

}

Основная часть программы.

while(scanf("%d %d %d",&a,&b,&k) == 3)

{

memset(f,0,sizeof(f));

res = calcTheSum(a,b,k);

printf("%lld\n",res);

}