1532. Рукопожатие
За круглым
столом собрались n бизнесменов. Перед
совещанием они должны одновременно пожать друг другу руки. Руки никаких
бизнесменов не должны пересекаться. Вычислить количество способов, которыми они
смогут пожать друг другу руки.
Вход. Каждая строка
содержит одно четное натуральное число n
(2 ≤ n ≤ 50).
Выход. Для каждого
значения n вывести в отдельной строке
количество способов, которыми n
бизнесменов смогут пожать друг другу руки.
|
Пример входа |
Пример выхода |
|
2 4 8 |
1 2 14 |
РЕШЕНИЕ
числа Каталана
Анализ алгоритма
Пронумеруем
бизнесменов, сидящих за столом, числами 1, 2, ..., 2 * p = n. Обозначим через f(p) количество
способов, которыми они могут пожать друг другу руки согласно условию задачи.
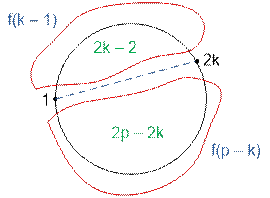
Рассмотрим все возможные рукопожатия первого бизнесмена. Он может протянуть
руку только тому бизнесмену, который имеет четный номер. Если первый бизнесмен протягивает
руку (2 * k) - ому, то с
одной стороны пересечения их рук останется 2 * k – 2 людей, которые могут
пожать руки f(k – 1) способами, а с другой стороны 2 * p – 2 * k
людей, которые могут пожать руки f(p – k) способами.
Выбирая k
= 1, 2, …, p, получим:
f(p) =
f(0) * f(p – 1) + f(1) * f(p – 2) + … + f(k – 1) * f(p
– k) + … + f(p – 1) * f(0),
f(1) = 1,
f(0) = 1
То есть f(p)
= 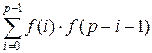 являются числами
Каталана.
являются числами
Каталана.
Ответом на
задачу будет значение f(n / 2).
Пример
Значения чисел
Каталана вычисляем в массиве cat по приведенной выше формуле:
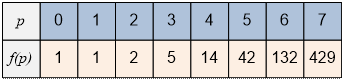
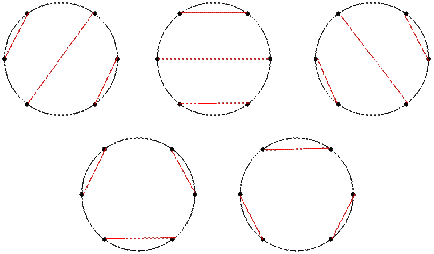
Например, n = 6 бизнесменов могут пожать
друг другу руки f(3) = 5 способами.
Реализация алгоритма
В ячейках cat[i]
будем вычислять i-ое число Каталана.
long long cat[51];
Используя рекуррентную формулу f(p) = 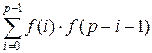 , функция countPerfect вычисляет числа
Каталана от нулевого до n-го.
, функция countPerfect вычисляет числа
Каталана от нулевого до n-го.
void countPerfect(int n)
{
int i, j;
cat[0] = cat[1] = 1;
for(i = 2; i
<= n; i++)
for(j = 0;
j < i; j++)
cat[i] += cat[j] * cat[i - j - 1];
}
Основной цикл программы. Для каждого входного значения n выводим cat[n / 2].
countPerfect(50);
while(scanf("%d",&n)
== 1)
printf("%lld\n",cat[n/2]);
Java реализация
import java.util.*;
public class
Main
{
static long[]
countPerfect(int n)
{
int i, j;
long cat[]= new long[51];
cat[0] = cat[1] = 1;
for(i = 2; i <= n; i++)
for(j = 0; j < i; j++)
cat[i] += cat[j] * cat[i - j - 1];
return cat;
}
public static void main(String[] args)
{
long cat[] = countPerfect(50);
Scanner con = new
Scanner(System.in);
while(con.hasNext())
{
int n = con.nextInt();
System.out.println(cat[n/2]);
}
}
}