1532. Handshake
Consider a meeting of n businessmen
sitting around a circular table. To start the meeting, they must shake hands.
Each businessman shakes the hand of exactly one other businessman. All
handshakes happen simultaneously. We say that the shake is perfect if no arms
cross each other.
Find the number of perfect shakes that
exist for n businessmen.
Input. Each line contains one even integer n (2 ≤ n
≤ 50).
Output. For each value of n print in a separate line
the number of perfect shakes that exist for n businessmen.
|
Sample
input |
Sample output |
|
2 4 8 |
1 2 14 |
SOLUTION
Catalan numbers
Algorithm
analysis
Let’s number the
businessmen sitting at the table with numbers 1, 2, ..., 2 * p = n.
Denote by f(p) the number of ways in which they can shake hands
according to the condition of the problem. Consider all possible handshakes of
the first businessman. He can only extend his hand to the businessman who has
an even number. If the first businessman extends his hand to (2 * k) - th, then from one side of their hands intersection
there will be 2 * k – 2
people who can shake hands in f(k – 1) ways, and on the other side 2 * p – 2 * k people who can shake hands in f(p
– k) ways.
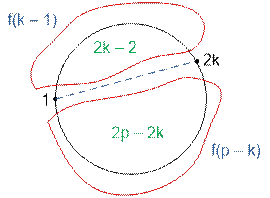
Choosing k = 1, 2, …, p,
we get:
f(p) =
f(0) * f(p – 1) + f(1) * f(p – 2) + … + f(k – 1) * f(p
– k) + … + f(p – 1) * f(0),
f(1) = 1, f(0) =
1
That is, f(p) = 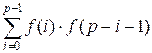 are Catalan numbers.
are Catalan numbers.
The answer to
the problem is
the
value f(n / 2).
Example
The values of
the Catalan numbers are calculated in the cat array according to the formula above:
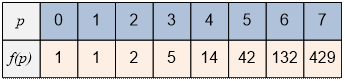
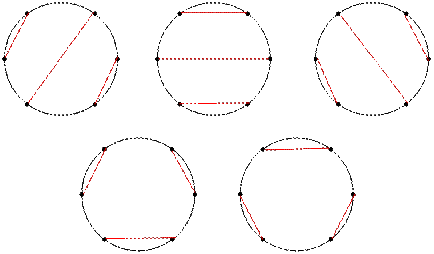
For example, n
= 6 businessmen can shake hands
in f(3) = 5 ways.
Algorithm
realization
In the cat[i] cells, we will calculate the i-th
Catalan number.
long long cat[51];
Using the recursive formula f(p) = 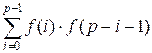 , function countPerfect finds the Catalan numbers from zero
to n-th.
, function countPerfect finds the Catalan numbers from zero
to n-th.
void countPerfect(int n)
{
int i, j;
cat[0] = cat[1] = 1;
for(i = 2; i <= n; i++)
for(j = 0; j < i; j++)
cat[i] += cat[j] * cat[i - j - 1];
}
The main part of the program. For each input value n print cat[n / 2].
countPerfect(50);
while(scanf("%d",&n)
== 1)
printf("%lld\n",cat[n/2]);
Java realization
import java.util.*;
public class Main
{
static long[] countPerfect(int n)
{
int i, j;
long cat[]= new long[51];
cat[0] = cat[1] = 1;
for(i = 2; i <= n; i++)
for(j = 0; j < i; j++)
cat[i] += cat[j] * cat[i - j - 1];
return cat;
}
public static void main(String[] args)
{
long cat[] = countPerfect(50);
Scanner con = new Scanner(System.in);
while(con.hasNext())
{
int n = con.nextInt();
System.out.println(cat[n/2]);
}
}
}