1535. Skyscrapers
The skyline of
the city has n buildings all in a
straight line; each building has a distinct height between 1 and n, inclusive. The building at index i is considered visible from the left if
there is no building with a smaller index that is taller. Similarly, a building
is visible from the right if there is no taller building with a higher index.
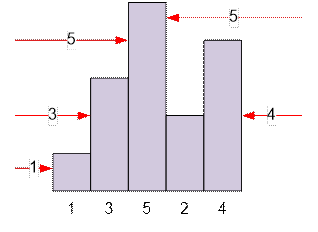
For example, if the buildings in order are {1, 3, 5, 2, 4},
then three buildings are visible from the left (1, 3, 5), but only
two are visible from the right (4 and 5).
You will be given
the total number of buildings n, l buildings visible from the left, and r buildings visible from the right.
Find the number of permutations of the buildings that are consistent with these
values.
Input. Each line is a
separate test case that contains the values of n (1 ≤ n ≤ 100), l and r (1 ≤ l, r
≤ n).
Output. For each
test case print in a separate line the number of permutations of the buildings
that are consistent with the given values. The results must be printed
modulo 109 + 7.
|
Sample
input |
Sample
output |
|
4 2 2 5 3 2 8 3 2 |
6 18 4872 |
SOLUTION
dynamic
programming
Algorithm
analysis
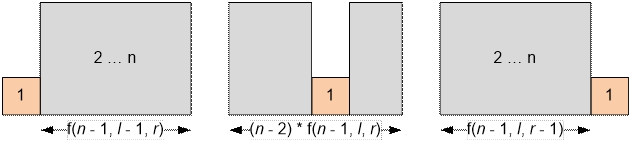
Suppose it
remains to arrange n houses, l of which should be visible from the left, and r from the right. Let
its possible
to do in f(n, l,
r) ways. Consider the house with the smallest height. If you put
it on the left, then it will always be visible, and the remaining houses can be
arranged in f(n – 1, l – 1, r) ways. If the
house with the smallest height is placed on the right, then it will always
remain visible on the right, the rest of the houses can be arranged in f(n
– 1, l, r – 1) ways. The smallest house can be placed between the other houses in n – 2 ways. In this case it will not be
visible, so the remaining houses can be arranged in (n
– 2) * f(n – 1, l, r) ways.
Note that for n = 1 the only possible arrangement will
be only for l = r = 1. We
obtain the recurrence relation:
f(n, l,
r) = f(n – 1, l – 1, r) + f(n – 1, l, r – 1) + (n – 2) * f(n – 1, l, r),
f(1, 1, 1) = 1,
f(1, x, y)
= 0, when x and y are not simultaneously equal to 1
Example
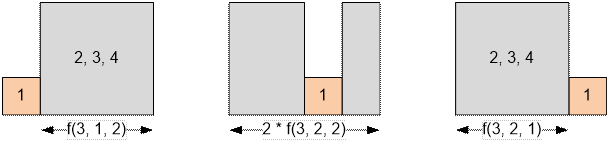
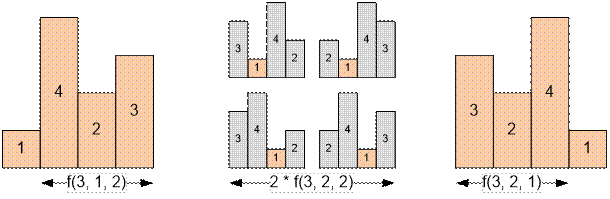
Construct all permutations
of houses for n = 4, l = 2, r = 2.
f(4, 2, 2) = f(3, 1, 2) +
2 * f(3, 2, 2) + f(3, 2, 1) = 1 + 2 * 2 + 1 = 6
Algorithm realization
Declare a
three-dimensional array dp, where dp[i][j][k] will store the value f(i,
j, k).
#define MAX 101
int dp[MAX][MAX][MAX];
Function f returns the number of ways that n houses can be arranged so that l can be visible from the left and r houses can be visible from the right.
long long f(int n, int l, int r)
{
if (n == 1) return (l == 1 && r == 1) ? 1 : 0;
if ((l <
1) || (r < 1)) return 0;
if (dp[n][l][r] != -1) return dp[n][l][r];
dp[n][l][r] = (f(n - 1, l - 1, r) + f(n - 1, l, r - 1) + (n - 2)*f(n - 1, l, r)) % 1000000007;
return dp[n][l][r];
}
The main part of the program. Read the input data. Compute and print the
answer.
while (scanf("%d %d %d", &n, &l, &r) == 3)
{
memset(dp, -1, sizeof(dp));
res = f(n, l, r);
printf("%d\n", res);
}
Java realization
import
java.util.*;
public class Main
{
static long dp[][][] = new long[101][101][101];
public static long f(int n, int l, int r)
{
if (n == 1) return (l == 1 && r == 1) ? 1 : 0;
if (l < 1 || r < 1) return 0;
if (dp[n][l][r] != -1) return dp[n][l][r];
dp[n][l][r] = (f(n - 1, l - 1, r) + f(n - 1, l, r - 1) + (n - 2)*f(n - 1, l, r)) % 1000000007;
return dp[n][l][r];
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
while (con.hasNextInt())
{
int n = con.nextInt();
int l = con.nextInt();
int r = con.nextInt();
for(int i = 0; i < 101; i++)
for(int j = 0; j < 101; j++)
for(int k = 0; k < 101; k++)
dp[i][j][k] = -1;
long res = f(n, l, r);
System.out.println(res);
}
con.close();
}
}