1539. Сколько точек пересечения?
Имеются две строки. На верхней строке отмечено a точек, а на нижней b точек. Соединим отрезком каждую точку
верхней строки с каждой точкой нижней строки. Точки расположены так, что
количество точек, полученных в результате пересечения отрезков, максимально.
Для достижения этой цели достаточно чтобы никакие три отрезка не пересекались в
одной точке. Точки на верхней и нижней строках в подсчет не включаются, в них
могут пересекаться любое количество отрезков. По значениям a и b Вам необходимо
вычислить P(a, b) – максимальное количество точек пересечения, расположенное между
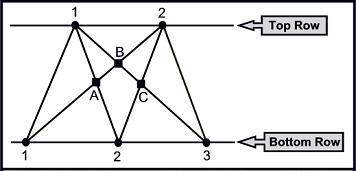
двумя строками. Например, пусть a = 2
и b = 3. Из рисунка видно, что P(2,
3) = 3.
Вход. Каждая строка
содержит два натуральных числа a (0
< a ≤ 20000) и b (0 < b ≤ 20000). Последний тест содержит два нуля и не
обрабатывается. Входные данные содержат не более 1200 тестов.
Выход. Для каждого
теста в отдельной строке вывести его номер и значение P(a, b). Результат
помещается в 64-битовое знаковое целое.
|
Пример
входа |
Пример
выхода |
2 22 33 3
0 0 |
Case 1: 1 Case 2: 3 Case 3: 9 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Обозначим через
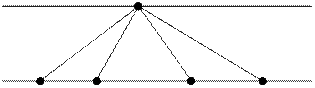
f(a, b) искомое количество точек пересечения. Очевидно, что f(1, b)
= 0, так как при a = 1 никакие два отрезка не пересекаются:
Рассмотрим общий
случай. Пусть x1, x2, …, xa
– точки на первой прямой, y1,
y2, …, yb – точки на второй прямой.
Соединим точку x1 с точками y1, y2,
…, yb. На отрезке x1y1
точек пересечения не будет. На отрезке x1y2
будут лежать точки пересечения с отрезками y1x2,
y1x3, …, y1xa
(всего a – 1 точек). На отрезке x1yj
будут лежать точки пересечения с отрезками yixk,
где i < j, 2 £ k £ a (всего (j – 1) * (a – 1) точек).
Количество точек пересечения, которые лежат на отрезках исходящих из x1,
равно (0 + 1 + 2 + … + (b – 1)) * (a – 1) = b * (b
– 1) / 2 * (a – 1).

Итак, из f(a,
b) точек b * (b – 1) / 2 * (a – 1) точек лежат на
отрезках исходящих из x1, а остальные точки лежат на отрезках
с концами в x2, …, xa. Имеем рекуррентное
соотношение:
f(a, b)
= b * (b – 1) / 2 * (a – 1) + f(a – 1, b)
Развернув его,
получим:
f(a, b)
= b * (b – 1) / 2 * (a – 1) + f(a – 1, b) =
b * (b –
1) / 2 * (a – 1) + b * (b – 1) / 2 * (a – 2) + f
(a – 2, b) = ... =
b * (b –
1) / 2 * (a – 1) + b * (b – 1) / 2 * (a – 2) + ... + b * (b – 1) / 2 * 1 =
b * (b –
1) / 2 * ( (a – 1) +
(a – 2) + ... + 1) =
b * (b –
1) / 2 * a * (a – 1) / 2
Таким образом,
максимальное количество точек пересечения равно
![]() *
* ![]()
Пример
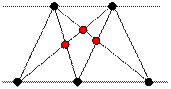
Рассмотрим
второй тест, для которого a = 2, b = 3. Максимально возможное
количество точек пересечения отрезков равно 3 и показано на рисунке:
Реализация алгоритма
Читаем входные
данные и для каждого теста вычисляем результат по выше приведенной формуле. При
заданных ограничениях на a и b в умножении переполнения не будет,
если вычисления проводить в 64-битовом целочисленном типе.
cs = 1;
while(scanf("%lld
%lld",&a,&b), a + b > 0)
{
res = a * (a - 1) * b * (b - 1) / 4;
printf("Case
%d: %lld\n",cs++,res);
}
Java
реализация
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int cs = 1;
while(true)
{
long a = con.nextLong();
long b = con.nextLong();
if (a + b == 0) break;
long res = a * (a - 1) * b * (b - 1) / 4;
System.out.println("Case " + cs++ + ": " + res);
}
con.close();
}
}