1539. How many points of intersection?

We have two rows. There are a dots on the top row and b dots on the bottom row. We draw line segments connecting every dot on the top row with every dot on the bottom row. The dots are arranged in such a way that the number of internal intersections among the line segments is maximized. To achieve this goal, we must not allow more than two segments to intersect in a point. The intersection points on the top row and the bottom are not included in our count; we can allow more than two segments to intersect on those two rows. Given the value of a and b, your task is to compute P(a, b), the number of intersections in between the two rows. 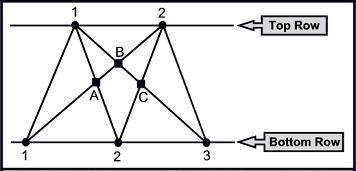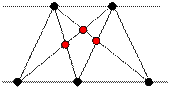For example, in the following figure a = 2 and b = 3. This figure illustrates that P(2, 3) = 3.

Input. Each line contains two positive integers a (0 < a ≤ 20000) and b (0 < b ≤ 20000). Input is terminated by a line where both a and b are zero. This case should not be processed. You will need to process at most 1200 sets of inputs.

Output. For each test case print in a line its serial number followed by the value of P(a, b). Look at the sample output for details. You can assume that the output for the test cases will fit in 64-bit signed integers.

Sample input	Sample output
2 2 2 3 3 3 0 0	Case 1: 1 Case 2: 3 Case 3: 9

SOLUTION

combinatorics

Algorithm analysis

Let f(a, b) be the required number of intersection points. Obviously, f(1, b) = 0, since for a = 1 no two segments intersect.

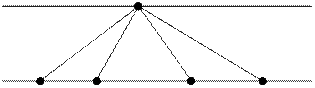
Consider the general case. Let x₁, x₂, …, x_a be points on the first line, y₁, y₂, …, y_b be points on the second line. Connect point x₁ with poinys y₁, y₂, …, y_b. There will be no intersection points on the segment x₁y₁. The segment x₁y₂ will contain the points of intersection with the segments y₁x₂, y₁x₃, …, y₁x_a (a – 1 points in total). The segment x₁y_j will contain the points of intersection with the segments y_ix_k, where i < j, 2 £ k £ a ( (j – 1) * (a – 1) points in total). The number of intersection points that lie on the segments outgoing from x₁ is (0 + 1 + 2 + … + (b – 1)) * (a – 1) = b * (b – 1) / 2 * (a – 1).

So, out of f(a, b) points b * (b – 1) / 2 * (a – 1) points lie on segments outgoing from x₁, and the rest of the points lie on segments with ends at x₂, …, x_a. We have a recurrent relation:

f(a, b) = b * (b – 1) / 2 * (a – 1) + f(a – 1, b)

Expanding it, we get:

f(a, b) = b * (b – 1) / 2 * (a – 1) + f(a – 1, b) =

b * (b – 1) / 2 * (a – 1) + b * (b – 1) / 2 * (a – 2) + f (a – 2, b) = ... =

b * (b – 1) / 2 * (a – 1) + b * (b – 1) / 2 * (a – 2) + ... + b * (b – 1) / 2 * 1 =

b * (b – 1) / 2 * ( (a – 1) + (a – 2) + ... + 1) =

b * (b – 1) / 2 * a * (a – 1) / 2

Thus, the maximum number of intersection points is

*

Example

Consider the second test case, where a = 2, b = 3. The maximum possible number of intersection points among the segments is 3 and this is shown in the figure:

Algorithm realization

Read the input data and for each test cae calculate the result according to the above formula. Given the constraints on a and b, there will be no overflow in multiplication if calculations are performed in a 64-bit integer type.

cs = 1;

while(scanf("%lld %lld",&a,&b), a + b > 0)

{

res = a * (a - 1) * b * (b - 1) / 4;

printf("Case %d: %lld\n",cs++,res);

}

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int cs = 1;

while(true)

{

long a = con.nextLong();

long b = con.nextLong();

if (a + b == 0) break;

long res = a * (a - 1) * b * (b - 1) / 4;

System.out.println("Case " + cs++ + ": " + res);

}

con.close();

}

}