1547. Ожерелье

 

Люди из некоторого племени делают ожерелья из глины. Ожерелье состоит из одного или более колец. Все кольца одного ожерелья имеют одинаковый диаметр и толщину. Например, ниже представлено ожерелье из четырех колец, длина которого в 4 раза больше диаметра одного кольца.

Пусть Vtotal – общий объем глины, имеющейся в наличии. Пусть V – объем глины, из которой делается одно кольцо, V0 – объем глины, теряемый в процессе его выпекания. Тогда диаметр D кольца равен

D =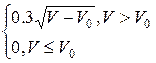

Если V £ V0, то кольцо не может быть сделано.

Рассмотрим пример, в котором Vtotal = 10, V0 = 1. Если делать из глины одно кольцо, то его диаметр будет равен D = 0.3 = 0.9. При изготовлении двух колец глину следует разделить на две части, объем каждой из которых равен V = Vtotal / 2 = 5. Из каждого куска можно сделать кольцо диаметром D = 0.3 = 0.6. Длина всего ожерелья будет равна 0.6 * 2 = 1.2.

Как видно из приведенного выше примера, длина ожерелья зависит от количества дисков в нем. В задаче необходимо найти такое количество колец, при изготовлении которых ожерелье будет иметь максимальную длину.

 

Вход. Каждая строка содержит два числа Vtotal (0 < Vtotal £ 60000) и V0 (0 < V0 £ 600). Последний тест содержит Vtotal = V0 = 0 и не обрабатывается.

 

Выход. Для каждого теста вывести количество колец, при котором ожерелье будет иметь максимальную длину. Если ответ определяется неоднозначно, или ожерелье создать нельзя, то вывести 0.

 

Пример входа

Пример выхода

10 1

10 2

0 0

5

0

 

 

РЕШЕНИЕ

математика

 

Анализ алгоритма

Пусть ожерелье будет самым длинным, если оно содержит n колец. Диаметр каждого кольца равен

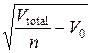D = 0.3 = 0.3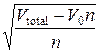

Длина всего ожерелья d равна

d = D * n = 0.3 = 0.3

Значение d будет максимальным, когда функция f(n) = Vn – V0n2 принимает наибольшее значение. Приравняем производную к 0: f’(n) = V – 2V0n = 0, откуда n = V / 2V0. Поскольку n является целым, то искомым n может быть как значение , так и . Вычисляем длину ожерелий при этих значениях n и находим наибольшую. Если длины одинаковы, то выводим 0 (число колец определяется не однозначно). Проверяем также возможность выпечки n колец из исходного количества глины: если Vtotal £ V0 * n, то сделать ожерелье невозможно.

 

Реализация алгоритма

Функция f вычисляет длину ожерелья, принимая на вход значения Vtotal, V0 и n.

 

double f(int v, int v0,int n)

{

  return 0.3 * sqrt(1.0 * v * n - v0 * n * n);

}

 

Основной цикл программы. Вводим значения Vtotal и V0, вычисляем значение n = . Проверяем возможность выпечки ожерелья для этого значения n. Вычисляем длину ожерелий для n =  и для n =  + 1, сравниваем и находим наибольшую из них. В случае равенства выводим 0.

 

while(scanf("%d %d",&v,&v0), v + v0 > 0)

{

  n = int(0.5 * v / v0);

  if (v <= v0 * n) {printf("0\n"); continue;}

  r1 = f(v,v0,n);

  r2 = f(v,v0,n+1);

  if (r2 > r1) n++;

  if (fabs(r1 - r2) < 1e-7) printf("0\n");

  else printf("%d\n",n);

}

 

Java реализация

 

import java.util.*;

 

public class Main

{

  public static double f(int v, int v0,int n)

  {

    return 0.3 * Math.sqrt(v * n - v0 * n * n);

  }

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);

    while(true)

    {

      int v = con.nextInt(), v0 = con.nextInt();

      if ((v == 0) && (v0 == 0)) break;

      int n = (int)(0.5 * v / v0);

      if (v <= v0 * n) {System.out.println("0"); continue;}

      double r1 = f(v,v0,n);

      double r2 = f(v,v0,n+1);

      if (r2 > r1) n++;

      if (Math.abs(r1 - r2) < 1e-7) System.out.println("0");

      else System.out.println(n);

    }

  }

}