1547. Necklace
The people of a certain tribe produce
circular ceramic discs with equal diameter by some rare clay. A necklace is
formed by connecting one or more discs. The thickness of each disc is fixed.
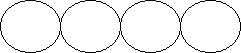
The figure below shows a necklace made with 4 discs. Its length is 4 times the
diameter of each disc.
Let Vtotal be the total volume of clay you have. The disk diameter
D and the volume of clay used V have the following relationship:
D =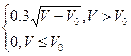 
,
where V0 is the volume lost
in the baking process from V unit of clay. When V ≤ V0, no
ceramic discs can be made.
As an example, let Vtotal = 10, V0 =
1. If we use it to make 1 disc, V = Vtotal
= 10, D = 0.3
= 0.9. If we divide the clay into 2 parts, the volume of
each part V = Vtotal / 2 =
5, and diameter of each disc formed is D = 0.3
= 0.6, thus the length of necklace formed this way is 0.6 *
2 = 1.2.
As explained in the above example, it
is obvious that the lengths of necklaces differ as the number of produced discs
changes. Write a program that computes the number of discs one should make so
that the longest possible necklace is formed.
Input. Each line contains two numbers Vtotal
(0 < Vtotal £ 60000) and V0 (0 < V0 £ 600), as defined above. Input ends
with a case where Vtotal = V0 = 0 that is not processed.
Output. Each output line should give the
number of discs one should make so that the necklace formed is the longest. If
this number is not unique, or no necklaces can be formed at all, print 0
instead.
|
Sample input |
Sample output |
|
10 1 10 2 0 0 |
5 0 |
SOLUTION
mathematics
Algorithm analysis
Assume that the longest necklace
contains n discs. The diameter of
each disk is
D = 0.3
= 0.3
The length d of the necklace equals to
d = D * n = 0.3
= 0.3
The
value d will be maximal when the
function f(n) = V
n – V0n2 takes the maximum value. Equate the derivative to 0:
f’(n) = V – 2V0n = 0, wherefrom n = V / 2V0. Since
n must be an integer, the value for n can be either 
or 
. Calculate the length of necklaces for these values
of n and choose the
maximum. If the lengths are the same, print 0 (the number of discs is not
uniquely defined). Check the possibility of producing n discs from the original amount of clay: if Vtotal £ V0 * n,
then it is impossible to make such a necklace.
Algorithm realization
The function f() calculates the
length of a necklace given the input values Vtotal,
V0 and n.
double f(int
v, int v0,int
n)
{
return 0.3 *
sqrt(1.0 * v * n - v0 * n * n);
}
The main part of the program. Read
the values Vtotal and V0, calculate the value n = . Check the possibility of baking the necklace for this value
n. Find the length of the necklaces
for n = and for n = + 1, compare them and
find the maximum. If the lengths are equal, print 0.
while(scanf("%d
%d",&v,&v0), v + v0 > 0)
{
n = int(0.5 *
v / v0);
if (v <=
v0 * n) {printf("0\n"); continue;}
r1 = f(v,v0,n);
r2 = f(v,v0,n+1);
if (r2 > r1)
n++;
if (fabs(r1 -
r2) < 1e-7) printf("0\n");
else printf("%d\n",n);
}