1548. Диагональ

Количество диагоналей в n-угольнике не менее N. Какое наименьшее значение может принимать n?

Вход. Содержит не более 1001 строк. В каждой строке записано натуральное число N (N £ 10¹⁵) – минимальное количество диагоналей. Последняя строка содержит 0 и не обрабатывается.

Выход. Для каждого теста в отдельной строке выведите его номер и наименьшее возможное значение n – количество сторон многоугольника.

Пример входа	Пример выхода
10 100 1000 0	Case 1: 7 Case 2: 16 Case 3: 47

РЕШЕНИЕ

математика

Анализ алгоритма

Каждая вершина выпуклого многоугольника соединена отрезками с остальными n – 1 вершинами. Из них два отрезка образуют стороны, а остальные n − 3 являются диагоналями. Так как всего вершин n, и из каждой выходит n − 3 диагонали, то общее число диагоналей в выпуклом n-угольнике равно n * (n – 3) / 2 (так как каждая диагональ учитывается дважды).

Если n * (n – 3) / 2 = N, то значение n можно найти из квадратного уравнения:

n² – 3 * n – 2 * N = 0

Положительный корень этого уравнения равен

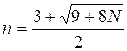
Остается округлить это значение вверх до ближайшего целого. Поскольку N £ 10¹⁵, все вычисления следует производить с использованием типа данных long long.

Пример

Рассмотрим второй тест. Для N = 100 получим

n = 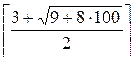= 16

Реализация алгоритма

Номер текущего теста будем хранить в переменной cs.

int cs = 1;

Читаем входные данные до тех пор, пока значение N больше нуля.

while(scanf("%lld",&n), n > 0)

{

Для каждого значения N вычисляем результат по формуле и выводим его вместе с номером теста.

res = int(ceil((3 + sqrtl(9.0 + 8*n)) / 2));

printf("Case %d: %d\n",cs,res);

cs++;

}

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

long n, cs = 1;

while((n = con.nextLong()) > 0)

{

long res = (int)(Math.ceil((3 + Math.sqrt(9 + 8*n))/2));

System.out.println("Case " + cs + ": " + res);

cs++;

}

}

}