1548. Diagonal

The number of diagonals in an n-gon is at least N. What is the smallest possible value that n can take?

Input. Contains no more than 1001 lines. Each line contains a positive integer N (N £ 10¹⁵) – the minimum number of diagonals. The last line contains 0 and should not be processed.

Output. For each test case, print its number and the smallest possible value of n – the number of sides of the polygon.

Sample input	Sample output
10 100 1000 0	Case 1: 7 Case 2: 16 Case 3: 47

SOLUTION

mathematics

Algorithm analysis

Each vertex of a convex polygon is connected by segments to the remaining n – 1 vertices. Among these, two segments form the sides of the polygon, and the remaining n – 3 are diagonals. Since there are nnn vertices in total, and each vertex is connected to n – 3 diagonals, the total number of diagonals in a convex n-gon is given by:

n * (n – 3) / 2

If n * (n – 3) / 2 = N, then the value of n can be found from the quadratic equation

n² – 3 * n – 2 * N = 0

The positive root of this equation is

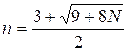
We round this value up to the nearest integer. Since N £ 10¹⁵, all computations should be performed using the long long data type.

Example

Let’s consider the second test case. For N = 100 we get:

n = 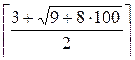= 16

Algorithm implementation

Store the current test number in the variable cs.

int cs = 1;

Read the input data as long as the value of N is greater than zero.

while(scanf("%lld",&n), n > 0)

{

For each value of N, compute the result using the formula and print it along with the test number.

res = int(ceil((3 + sqrtl(9.0 + 8*n)) / 2));

printf("Case %d: %d\n",cs,res);

cs++;

}

Java implementation

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

long n, cs = 1;

while((n = con.nextLong()) > 0)

{

long res = (int)(Math.ceil((3 + Math.sqrt(9 + 8*n))/2));

System.out.println("Case " + cs + ": " + res);

cs++;

}

}

}