1551. Исправить расстановку скобок

В заданной строке из скобок требуется изменить наименьшее количество символов так, чтобы полученная строка была правильной. Удалять или вставлять символы нельзя.

Всего имеется три вида скобок: обычные (), квадратные [] и фигурные {}. Каждая пара скобок содержит соответственно открывающийся ('(', '[', '{' ) и закрывающийся (')', ']', '}') символ.

Правильная строка определяется следующими правилами:

· Пустая строка является правильной.

· Если строка s правильная, то правильными являются также (s), [s] и {s}.

· Если строки s и t правильные, то правильной будет строка st.

Например, строки "([{}])", "" и "(){}[]" являются правильными, а "([}]", "([)]" и "{" нет.

Для заданной строки следует изменить наименьшее количество символов так, чтобы она стала правильной.

Вход. Каждая строка содержит четное количество символов '(', ')', '[', ']', '{', '}'. Длина каждой строки не более 50.

Выход. Для каждой скобочной записи вывести в отдельной строке наименьшее количество символов, которое можно изменить так, чтобы строка стала правильной.

Пример входа	Пример выхода
]()[((() ([)] ([{}[]	3 2 1

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Обозначим через f(i, j) наименьшее количество символов, которое можно изменить так, чтобы подстрока s_is_i+1…s_j-1s_j стала правильной. Тогда имеют место соотношения:

1. f(i, j) = 0 при i > j, так как в таком случае подстрока будет пустой.

2. f(i, j) = f(i + 1, j – 1) + enc(s_i ,s_j). Делаем так, чтобы символ s_i был открывающейся скобкой, а s_j – соответствующий ему закрывающейся скобкой. Далее рекурсивно рассматриваем подстроку s_i+1…s_j-1.

Функция enc(s_i ,s_j) возвращает:

а) 0, если символы s_i и s_j являются соответствующими открывающейся и закрывающейся скобками;

б) 2, если символ s_i является закрывающейся скобкой, а s_j – открывающейся;

в) 1 иначе. В этом случае достаточно изменить один из символов s_i или s_j так, чтобы они образовали правильную скобочную пару;

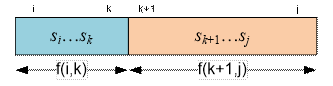
3. f(i, j) = (f(i, k) + f(k + 1, j)). Подстроку s_is_i+1…s_j-1s_j рассматриваем как последовательность двух правильных скобочных структур: s_i…s_k и s_k+1…s_j. Длина подстроки s_i…s_k должна быть четной, следовательно k принимает значения i + 1, i + 3, …, j – 2.

Пример

Рассмотрим первую строку из примера.

f(0, 7) = f(0, 3) + f(4, 7) = (2 + f(1, 2)) + (0 + f(5, 6)) = (2 + 0) + (0 + 1) = 3

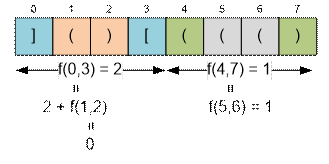
Реализация алгоритма

В ячейках m[i][j] массива m сохраняем значения f(i, j). Входную строку считываем в s.

int m[51][51], res;

string s;

Реализация функции enc(c, d).

int enc(char c, char d)

{

string p = "([{)]}";

Функция возвращает 2, если c является закрывающейся скобкой, а d открывающейся.

if (p.find(c) / 3 > 0 && p.find(d) / 3 < 1) return 2;

Функция возвращает 0, если c и d являются соответствующими скобками. Если они стоят не в правильном порядке, то функция вернет значение 2 в предыдущей строке.

if (p.find(c) % 3 == p.find(d) % 3 && c != d) return 0;

Во всех остальных случаях возвращаем 1.

return 1;

}

Функция f(i, j) возвращает наименьшее количество символов, которое можно изменить так, чтобы подстрока s_is_i+1…s_j-1s_j стала правильной.

int f(int i, int j)

{

if (i > j) return 0;

if (m[i][j] != -1) return m[i][j];

int r = f(i+1,j-1) + enc(s[i],s[j]);

for(int k = i + 1; k < j; k += 2)

r = min(r,f(i,k) + f(k+1,j));

return m[i][j] = r;

}

Основная часть программы. Обрабатываем несколько тестов.

while(cin >> s)

{

memset(m,-1,sizeof(m));

Ответом задачи будет значение f(0, |s| – 1), где s – входная строка.

res = f(0, s.size() - 1);

cout << res << endl;

}

Java реализация

import java.util.*;

public class Main

{

static int m[][];

static String s;

public static int enc(char c, char d)

{

String p = "([{)]}";

if (p.indexOf(c) / 3 > 0 && p.indexOf(d) / 3 < 1) return 2;

if (p.indexOf(c) % 3 == p.indexOf(d) % 3 && c != d) return 0;

return 1;

}

public static int f(int i, int j)

{

if (i > j) return 0;

if (m[i][j] != -1) return m[i][j];

int r = f(i + 1, j - 1) + enc(s.charAt(i), s.charAt(j));

for (int k = i + 1; k < j; k += 2)

r = Math.min(r, f(i, k) + f(k + 1, j));

return m[i][j] = r;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while (con.hasNext())

{

s = con.next();

int len = s.length();

m = new int[len][len];

for(int i = 0; i < len; i++)

for(int j = 0; j < len; j++)

m[i][j] = -1;

int res = f(0, len - 1);

System.out.println(res);

}

con.close();

}

}