1552. Fast Postman

A postman has to deliver several letters along a street. He has the address (in the form of the number of meters from the left end of the street to the destination of the letter) and the maximum time he can take to deliver each letter. The postman moves at 1 meter per second and can deliver a letter instantly once he reaches the right location. You need to find out if it's possible to make all the deliveries within the given constraints, and if so, the minimum time the postman can take to do it.

Input. Contains multiple test cases, each of them consists of three lines. In the first line of each test there are two numbers: the number of addresses AddrNum (1 ≤ AddrNum ≤ 50) and the initial position of the postman initialPos (1 ≤ initialPos ≤ 10⁶) in the same units and format as the addresses. The second and the third line contains AddrNum numbers. The i-th element of the second and the third line represents the address and maximum time of delivery of the i-th letter. Each number in the second line of the test is between 1 and 10⁶ inclusive. Each number in the third line of the test is between 1 and 10⁹ inclusive.

Output. For each test case print in a separate line the minimum amount of time the postman needs to deliver all letters within the given constraints or -1 if it's impossible to do so.

Sample input	Sample output
4 4 1 3 5 7 9 2 5 100 4 2 1 7 10 4 15 6 28 39	13 20

SOLUTION

dynamic programming

Algorithm analysis

Если почтальон на своем пути поравняется с некоторым домом, куда следует доставить письмо, то его следует отдавать сразу же, при первом же подходе к дому. Если почтальон уже разнес письма в i - ый и j - ый дома, то он точно уже разнес письма во все дома, которые находятся между i - ым и j - ым домом. Таким образом, множество домов, куда уже разнесена почта, представляет собой отрезок прямой с точкой initialPos внутри. Следует также отметить, что направление движения почтальон может менять только в точке с домом, в который он только что доставил письмо.

Состояние почтальона определим тройкой чисел:

1. левый конец интервала домов, куда уже разнесена почта;

2. правый конец интервала домов, куда уже разнесена почта;

3. текущее положение почтальона;

Вместо самих чисел в состоянии почтальона лучше хранить их индексы в массиве address. На каждом шаге (i, j, k) следует определить, куда лучше двигаться почтальону: вправо (i, j + 1, j + 1) или влево (i – 1, j, i – 1). Также заметим, что для каждого состояния (i, j, k) текущее положение почтальона k равно i или j.

В ячейках sol[i][j][0] будем хранить наименьшее время, за которое почтальон разнесет все письма в дома в интервале (i, j), причем находиться будет в точке i (в левом конце интервала). Соответственно в sol[i][j][1] будет содержаться та же информация, только почтальон будет находиться в правом конце интервала – в точке j.

Отсортируем адреса домов по возрастанию их координат. Чтобы при сортировке соответствующим образом переставлялось и граничное время доставки, создадим вектор пар houses, первый элемент которого содержит адрес дома, а второй – максимальное время доставки письма в этот дом. При сортировке вектора пар по возрастанию сортировка производится по первой компоненте – то есть по расстоянию от левого края улицы.

Инициализация массива sol:

sol[i][i][0] = sol[i][i][1] = | address[i] – initialPos | = | houses[i].first – initialPos |

Для доставки письма в единственный дом, индекс которого равен i, необходимо затратить время, равное расстоянию от начального положения initialPos до местоположения дома address[i].

Рассмотрим интервал (i, j). Почтальон может оказаться в его левом конце, двигаясь либо с левого конца интервала (i + 1, j), либо с правого конца интервала (i + 1, j). В первом случае ему требуется пройти расстояние address[i + 1] – address[i], во втором address[j] – address[i]. То есть

sol[i][j][0] = min(sol[i + 1][j][0] + address[i + 1] – address[i],

sol[i + 1][j][1] + address[j] – address[i])

Аналогично почтальон может оказаться в правом конце итервала (i, j), если он будет двигаться либо с левого конца интервала (i, j – 1), либо с правого конца интервала (i, j – 1). В первом случае ему требуется пройти расстояние address[j] – address[i], во втором address[j] – address[j – 1]. Таким образом

sol[i][j][1] = min(sol[i][ j – 1][0] + address[j] – address[i],

sol[i][ j – 1][1] + address[j] – address[j – 1])

Если на каком-нибудь этапе вычисления значение sol[i][j][0] (или sol[i][j][1]) станет большим maxTime[i] (или соответственно maxTime[j]), то установим его равным плюс бесконечности (значению INF = 2000000000). Последнее означает тот факт, что добраться до соответствующего дома в отведенное время почтальон не может.

Почтальон доставит все письма, когда будут пройдены все дома из интервала (0, n – 1), где n – количество домов. При этом нам не важно, в каком из концов этого интервала закончит путь почтальон. То есть ответом будет значение

min(sol[0][n – 1 ][0], sol[0][n – 1][1])

Если это значение равно плюс бесконечности, то разнести письма в срок не удастся и следует вернуть -1 как требуется в условии задачи.

Example

Рассмотрим первый тест. Красным отображен весь путь почтальона.

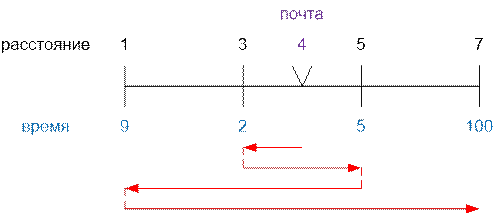
Рассмотрим значения sol для интервала [3; 5].

· В точку 3 можно попасть по пути 4 → 5 → 3, sol[3][5][0] = 1 + 2 = 3;

· В точку 5 можно попасть по пути 4 → 3 → 5, sol[3][5][1] = 1 + 2 = 3;

Однако поскольку имеется ограничение по времени на доставку в точку 3 (не более 2 секунд), то будет установлено sol[3][5][0] = +∞.

Рассмотрим значения sol для интервала [1; 5].

· Двигаться в 1 из 3 мы не можем, так как sol[3][5][0] = +∞. Поэтому попасть в 1 можно только из правого конца интервала [3; 5]:

sol[1][5][0] = sol[3][5][1] + |5 – 1| = 3 + 4 = 7;

· Попасть в правый конец интервала [1; 5] можно только из концов интервала [1; 3]:

sol[1][5][1] = min(sol[1][3][0] + |5 – 1|, sol[1][3][1] + |5 – 3|) =

min(3 + |5 – 1|, 5 + |5 – 3|) = min(7, 7) = 7

Из-за ограничения по времени доставки в точку 5 (не более 5 секунд) будет установлено sol[1][5][1] = +∞.

Algorithm realization

Объявим необходимые массивы и переменные.

int sol[50][50][2];

int i, res, Num, value, InitPos;

vector<int> address, maxTime;

Функция minTime возвращает наименьшее возможное время доставки всех писем при заданных ограничениях.

int minTime(void)

{

int res, i, j, n = address.size();

Создаем массив пар houses, содержащий адреса и время доставки писем. Сортируем пары по адресам.

vector<pair<int,int> > houses;

for(i = 0; i < n; i++)

houses.push_back(make_pair(address[i],maxTime[i]));

sort(houses.begin(),houses.end());

Инициализируем массив sol.

memset(sol,0,sizeof(sol));

for(i = 0; i < n; i++)

{

sol[i][i][0] = sol[i][i][1] = abs(houses[i].first - InitPos);

if (sol[i][i][0] > houses[i].second)

sol[i][i][0] = sol[i][i][1] = INF;

}

Заполняем ячейки массива sol.

for(i = n - 1; i >= 0; i--)

for(j = i + 1; j < n; j++)

{

sol[i][j][0] = min(sol[i+1][j][0] + houses[i+1].first –

houses[i].first, sol[i+1][j][1] + houses[j].first - houses[i].first);

if (sol[i][j][0] > houses[i].second) sol[i][j][0] = INF;

sol[i][j][1] = min(sol[i][j-1][0] + houses[j].first –houses[i].first, sol[i][j-1][1] + houses[j].first - houses[j-1].first);

if (sol[i][j][1] > houses[j].second) sol[i][j][1] = INF;

}

Вычисляем ответ.

res = min(sol[0][n-1][0],sol[0][n-1][1]);

if (res == INF) return -1;

return res;

}

Основная часть программы.

while(scanf("%d %d",&Num,&InitPos) == 2)

{

address.clear(); maxTime.clear();

for(i = 0; i < Num; i++)

scanf("%d",&value),address.push_back(value);

for(i = 0; i < Num; i++)

scanf("%d",&value),maxTime.push_back(value);

res = minTime();

printf("%d\n",res);

}