1559. Избирательная система

Студенты Байтляндского университета для занятий используют автоматическую систему регистрации. Регистрация открыта определенный период времени. При этом каждый момент времени имеет характеристику, которая описывается положительным числом. Входить в систему можно не более k раз, каждый вход может длиться не более d единиц времени. Периоды нахождения в системе не должны пересекаться.

Имеется строка, i - ый символ которой описывает характеристику в i - ый момент времени. Характеристика задается буквами от ‘a’ до ‘z’, обозначающих соответственно числа от 1 до 26. Необходимо разработать стратегию входа в систему, для которой сумма характеристик во время нахождения в системе наибольшая.

Вход. Первая строка каждого теста содержит значения d и k (1 ≤ d, k ≤ 1000). Вторая содержит строку, состоящую из не более чем 1000 букв ‘a’ – ‘z’.

Выход. Для каждого теста в отдельной строке выведите наибольшую возможную сумму характеристик.

Пример входа

4 1

acacca

2 2

cabcca

2 18

yptcsevnuzlsrfjxurpslztlinhddelpitmvaezowjcfjjfgmfq

Пример выхода

10

10

598

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

В ячейках s[i] будем хранить сумму характеристик всех моментов времени от 1 до i – го (префиксные суммы). В dp[i][j] будет находиться наибольшая возможная сумма характеристик периодов времен при условии, что уже прошло i единиц времени, а в систему входили в точности j раз.

Рассмотрим два случая:

· Если в i - ый момент времени студент не находится в системе, то dp[i][j] = dp[i – 1][j]. Это означает, что j раз входили в систему в период до (i – 1)-ой единицы времени включительно.

· Поскольку значения всех характеристик положительны, то чем больше мы будем в системе, тем большей будет сумма характеристик. Если в i - ый момент времени студент находится в системе, то считаем, что вошел он туда в (i – d + 1) - ый момент времени. В этом случае

dp[i][j] = dp[i – d][j – 1] + s[i] – s[i – d]

Заметим, что разница s[i] – s[i – d] равна сумме характеристик с (i – d + 1) - го по i - ый момент времени. Например, при d = 2, i = 5, s[5] – s[3] содержит сумму характеристик для 4 и 5 момента времени.

Тогда имеет место соотношение:

dp[i][j] = max{dp[i – d][j – 1] + s[i] – s[i – d], dp[i – 1][j]}

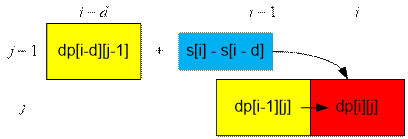
При этом значение i – d считается равным нулю, если i – d < 0.

Также отметим, что dp[i][0] = 0, так как если в систему не входили ни одного раза, то максимальная сумма характеристик равна нулю.

Пример

Рассмотрим второй пример, в котором d = 2, k = 2. По строке “cabcca” заполним массив s:

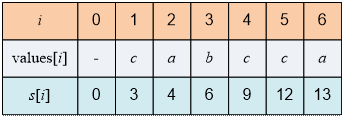
Поскольку длина строки равна 6, а k = 2, то размер массива dp будет 6 на 2. Следующая таблица содержит значения ячеек двумерного массива dp[i][j].

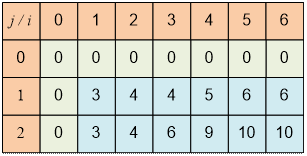
Например:

dp[4][1] = max{dp[2][0] + s[4] – s[2], dp[3][1]} =

max{0 + 9 – 4, 4} = max{5, 4} = 5

dp[5][2] = max{dp[3][1] + s[5] – s[3], dp[4][2]} =

max{4 + 12 – 6, 9} = max{10, 9} = 10

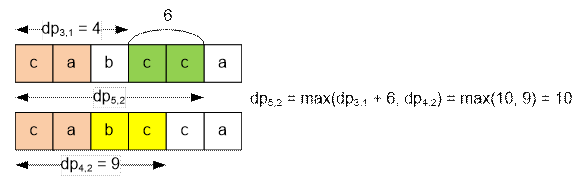
Поскольку максимум достигается на значении dp[3][1] + s[5] – s[3], то студенту в момент времени 5 выгоднее быть в системе. То есть его второе вхождение в систему (когда прошло еще не более пяти секунд) должно происходить в моменты времени 4 и 5.

Реализация алгоритма

Объявим рабочие массивы.

int s[1001], dp[1001][1001];

Функция maximalGoodness возвращает наибольшую возможную сумму характеристик.

int maximalGoodness(int d, int k)

{

int i, j, temp, n = str.size();

Вычислим сумму характеристик всех моментов времени от 1 до i - го и занесем ее в s[i].

memset(s,0,sizeof(s));

for(i = 1; i <= n; i++)

s[i] = s[i-1] + str[i-1] - 'a' + 1;

Вычисляем значения dp[i][j].

memset(dp,0,sizeof(dp));

for(i = 1; i <= n; i++)

for(j = 1; j <= k; j++)

{

temp = (i - d) < 0 ? 0 : i - d;

dp[i][j] = max(dp[i-1][j],dp[temp][j-1] + s[i] - s[temp]);

}

return dp[n][k];

}

Основная часть программы. Обрабатываем несколько тестов.

while (cin >> d >> k)

{

cin >> str;

res = maximalGoodness(d, k);

cout << res << endl;

}