1560. Уменьшающееся число
Над целым числом можно
производить следующие операции:
· Если число делится на 3,
то разделить его на 3;
· Если число делится на 2,
то разделить его на 2;
· Вычесть 1.
По заданному натуральному
числу n найдите наименьшее количество
операций, после выполнения которых получится 1.
Вход. Каждая строка содержит одно натуральное число n (1 ≤ n ≤ 106).
Выход. Для каждого значения n
в отдельной строке выведите наименьшее количество операций, после выполнения которых
получится 1.
|
Пример
входа |
Пример
выхода |
|
1 5 10 |
0 3 3 |
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Пусть f(n) содержит наименьшее количество операций, выполнение которых
преобразует число n в 1. Например,
·
f(1) = 0, так как мы уже имем число 1;
·
f(2) = 1, преобразование
2 → 1;
·
f(5) = 3, преобразование 5 → 4 → 2 → 1;
·
f(10) = 3, преобразование 10 → 9 → 3 → 1;
В случае n = 10 выгоднее сначала вычесть 1, нежели воспользоваться идеей
жадности и разделить на 2.
Рассмотрим
процесс вычисления функции f(n).
·
Если разделить число n
на 3 (при условии что n делится на
3), то
f(n) = f(n / 3) + 1
·
Если разделить число n
на 2 (при условии что n делится на
2), то
f(n) = f(n / 2) + 1
·
Если из числа n
вычесть 1, то
f(n) = f(n – 1) + 1
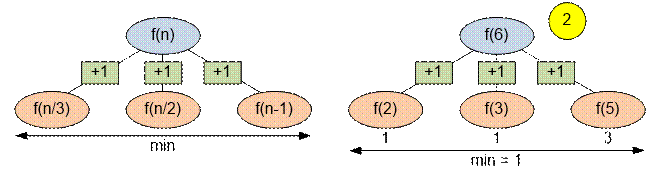
Из числа n можно получить одно из трех чисел: n / 3, n / 2 или n – 1. Количество
операций, за которое каждое из этих чисел можно свести к 1, равно f(n / 3), f(n / 2) и f(i – 1)
соответственно. Поскольку нас интересует наименьшее количество операций, то имеем
следующее
соотношение:
f(n) = min(f(n – 1), f(n / 2), f(n / 3)) + 1,
f(1) = 0
При этом если n не делится на 2 (или на 3), то
соответствующий элемент (f(n / 2) или
f(n / 3)) отсутствует в функции min.
Например, для n = 8 имеем:
f(8) = min(f(7), f(4)) + 1
Соответственно для n = 7 получим:
f(7) = min(f(6)) + 1 = f(6)
+ 1
Значения функции
f(n) будем запоминать в ячейках массива d[MAX], где MAX = 106 + 1. Заполняем ячейки массива d
от 1 до 106 согласно приведенному рекуррентному соотношению.
Например, в следующей таблице приведены значения d[i] для 1 £ i £ 11:

Например,
d[10] = min(d[9], d[5]) +
1 = min(2, 3) + 1 = 3
То есть нам эффективнее
вычитать из 10 единицу, нежели делить ее на 2.
Упражнение
Вычислите
значения d[i] для следующих значений i:

Реализация алгоритма
Объявим массив d, i-ая ячейка которого содержит наименьшее
количество операций, выполнение которых преобразует число i в 1.
#define MAX 1000001
int d[MAX];
Заполняем ячейки массива d согласно приведенным формулам.
for (i = 2; i < MAX; i++)
{
// d[i] =
min(d[i/3],d[i/2],d[i-1]) + 1
d[i] = d[i - 1];
if (i % 2 == 0) d[i] = min(d[i],
d[i / 2]);
if (i % 3 == 0) d[i] = min(d[i],
d[i / 3]);
d[i]++;
}
Для каждого входного
значения n выводим ответ d[n].
while(scanf("%d",&n) == 1)
printf("%d\n",d[n]);
Реализация алгоритма –
рекурсия
#include <stdio.h>
#include <string.h>
#define INF 2000000000
int i, res, n;
int dp[1000001];
int min(int a, int b, int c)
{
int res = a;
if (b < res) res = b;
if (c < res) res = c;
return res;
}
int f(int n)
{
if (n == 1) return 0;
if (dp[n] != -1) return dp[n];
int a = f(n - 1);
int b = (n % 2 == 0) ? f(n / 2) : INF;
int c = (n % 3 == 0) ? f(n / 3) : INF;
return dp[n] = min(a,b,c)
+ 1;
}
int main(void)
{
memset(dp, -1, sizeof(dp));
while (scanf("%d", &n) == 1)
{
res = f(n);
printf("%d\n", res);
}
return 0;
}
Java реализация
import java.util.*;
public class
{
public static int MAX = 1000001;
static int d[] = new int[MAX];
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
d[1] = 0;
for(int i = 2; i < MAX; i++)
{
d[i] = d[i-1] + 1;
if (i % 2 == 0) d[i] = Math.min(d[i], d[i/2] + 1);
if (i % 3 == 0) d[i] = Math.min(d[i], d[i/3] + 1);
}
while(con.hasNext())
{
int n = con.nextInt();
System.out.println(d[n]);
}
}
}
Python реализация
Создадим список d, i-ая ячейка которого содержит наименьшее количество операций,
выполнение которых преобразует число i
в 1.
d = [0] * 1000001
Заполняем ячейки массива d согласно приведенным формулам.
d[1] = 0
for i in range(2, 1000001):
d[i] =
d[i - 1]
if i % 2 == 0
and d[i // 2] < d[i]:
d[i] =
d[i // 2]
if i % 3 == 0
and d[i // 3] < d[i]:
d[i] =
d[i // 3]
d[i] += 1
Для каждого входного
значения n выводим ответ d[n].
while True:
try:
n = int(input())
print(d[n])
except EOFError:
break