1561. Атака на RSA
Проблема RSA состоит в следующем: дано положительное целое
число n, которое является
произведением двух различных простых нечетных чисел p и q, положительное
целое e такое что НОД(e, (p
− 1) · (q − 1)) = 1, а
также целое c. Необходимо найти такое
положительное целое m, что me = c (mod n).
Вход. Первая строка содержит количество тестов k (k
≤ 2000). Каждая следующая строка является отдельным тестом и содержит три
числа e, n и c (e, n,
c ≤ 32000, n = p · q; p,
q – различные нечётные простые, НОД(e, (p
− 1) · (q − 1)) = 1, e < (p − 1) · (q −
1)).
Выход. Для каждого
теста в отдельной строке вывести значение m.
|
Пример
входа |
Пример
выхода |
|
3 9 187 129 11 221 56 7 391 204 |
7 23 17 |
РЕШЕНИЕ
теория чисел – RSA
Анализ алгоритма
Решение задачи основано
на циклической атаке. По известному шифру c (c = me
mod n) злодей, имея открытый ключ e и n, хочет найти
сообщение m. Он строит последовательность чисел
c, ce,
![]() ,
, ![]() , …
, …
Поскольку
вычисления совершаются в группе Zn*, то элементы последовательности
находятся в границах от 0 до n – 1. То есть существует такое натуральное
k, что с = ![]() . Поскольку c = me mod n, то me
=
. Поскольку c = me mod n, то me
= ![]() , или m =
, или m = ![]() .
.
Таким образом, для
нахождения сообщения m по его шифру c необходимо построить последовательность
c, ce, ![]() ,
, ![]() , …,
, …, ![]() ,
, ![]() = c, и взять ее
предпоследний член.
= c, и взять ее
предпоследний член.
Пример
Рассмотрим
уравнение m7 mod 323 = 251. Здесь e = 7, n =
323, c = 251.
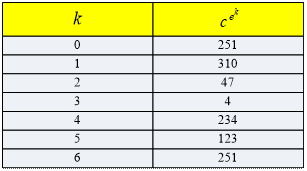
Из таблицы имеем:
c = ![]() = 251. Поскольку me
=
= 251. Поскольку me
= ![]() , то m =
, то m = ![]() = 123.
= 123.
Реализация алгоритма
Функция pow вычисляет значение bp
mod m.
int pow(int b, int p, int m)
Читаем входные
данные.
scanf("%d",&tests);
while(tests--)
{
scanf("%d %d
%d",&e,&n,&c);
Начальное значение шифра с сохраним в переменной cOriginal.
cOriginal = c;
c = pow(c,e,n); cPrev = cOriginal;
В начале i-ой итерации цикла while в переменной c содержится значение ![]() , а в переменной cPrev значение
, а в переменной cPrev значение ![]() . Цикл продолжается, пока не встретится такое k, для которого cOriginal =
. Цикл продолжается, пока не встретится такое k, для которого cOriginal = ![]() .
.
while(c !=
cOriginal)
{
cPrev = c;
c = pow(c,e,n);
}
По окончанию цикла искомое сообщение m находится в переменной cPrev, которое равно ![]() .
.
printf("%d\n",cPrev);
}