1562. Модулярные уравнения

Законы модулярной арифметики являются лучшим оружием в нашем арсенале. Мы, подражатели ученых, часто используем эти законы для управления миром. Например, если мы хотим вычислить

2³5¹³7¹⁴ – 2⁴5¹⁴7³²,

то это можно сделать в один миг. Однако для этого следует решить уравнения в модулярной арифметике, и многие из нас могут прийти в замешательство. Но не бойтесь; мы не будем устрашать Вас ужасной системой модулярных уравнений, мы дадим Вам простую задачку. По заданным интервалам трех целых чисел a (amin ≤ a ≤ amax), b (bmin ≤ b ≤ bmax) и m (mmin ≤ m ≤ mmax) Вам следует найти количество таких троек (a, b, m), которые удовлетворяют уравнению:

(a + b) mod m = (a – b) mod m

Рассмотрим пример.

1 ≤ a ≤ 2, 2 ≤ b ≤ 4, 3 ≤ m ≤ 5

(1 + 2) mod 4 = 3 = (1 – 2) mod 4

(1 + 3) mod 3 = 1 = (1 – 3) mod 3

(1 + 4) mod 4 = 1 = (1 – 4) mod 4

(2 + 2) mod 4 = 0 = (2 – 2) mod 4

(2 + 3) mod 3 = 2 = (2 – 3) mod 3

(2 + 4) mod 4 = 2 = (2 – 4) mod 4

Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 20). Каждая из следующих t строк является отдельным тестом и содержит три пары целых чисел amin, amax, bmin, bmax и mmin, mmax. Известно, что -1000 ≤ amin ≤ amax ≤ 1000, -1000 ≤ bmin ≤ bmax ≤ 1000, 1 ≤ mmin ≤ mmax ≤ 1000.

Выход. Для каждого теста вывести в отдельной строке его номер и количество троек (a, b, m), удовлетворяющих модулярному уравнению.

Пример входа	Пример выхода
3 1 2 2 4 3 5 -100 100 200 350 1 1000 5 9 10 12 2 9	Case 1: 6 Case 2: 318384 Case 3: 45

РЕШЕНИЕ

теория чисел – модулярная арифметика

Анализ алгоритма

Поскольку выражения a + b и a – b дают одинаковые остатки при делении на m, то их разница a + b – (a – b) = 2b делится на m. Задача свелась к поиску таких пар (b, m) из заданного интервала, для которых 2b делится на m.

Если m – нечетное, то b должно делиться на m. Количество таких b из интервала [bmin, bmax] равно

–

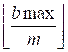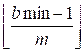
Если m – четное, то b должно делиться на m / 2. Количество таких b из того же интервала равно

–

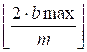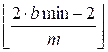
Для каждого m Î [mmin, mmax] вычисляем и суммируем такое количество b. Поскольку для каждой пары (b, m), для которой 2b делится на m, любое a (количество возможных a равно amax – amin + 1) может образовать искомую тройку чисел (a, b, m), то найденное количество b следует умножить на (amax – amin + 1).

Пример

Рассмотрим первый тест, для которого 1 £ a £ 2, 2 £ b £ 4, 3 £ m £ 5. Переберем значения m:

m = 3 (нечетное). Имеется лишь одно b = 3, которое делится на m. Паре (b, m) = (3, 3) соответствуют решения

(1 + 3) mod 3 = (1 – 3) mod 3, (2 + 3) mod 3 = (2 – 3) mod 3

m = 4 (четное). Имеются два значения b, которые делятся на m / 2 = 2. Паре (b, m) = (2, 4) соответствуют решения

(1 + 2) mod 4 = (1 – 2) mod 4, (2 + 2) mod 4 = (2 – 2) mod 4

а паре (b, m) = (4, 4) решения

(1 + 4) mod 4 = (1 – 4) mod 4, (2 + 4) mod 4 = (2 – 4) mod 4

m = 5 (нечетное). В допустимом интервале для переменной не существует ни одного числа b, которое делится на 5. Поэтому для m = 5 решений нет.

Итого имеется 6 троек, удовлетворяющих первому тесту.

Реализация алгоритма

Обнуляем переменную res, в которой будет содержаться количество троек, удовлетворяющих условию задачи. Читаем входные данные.

res = 0;

scanf("%d %d %d %d %d %d",&amin,&amax,&bmin,&bmax,&mmin,&mmax);

Перебираем все возможные значения m, для каждого из них по формулам вычисляем количество таких b, для которых 2b делится на m.

for(m = mmin; m <= mmax; m++)

if (m % 2)

res += (int)floor(1.0*bmax/m) - (int)floor((1.0*bmin-1)/m);

else res += (int)(floor(2.0*bmax/m)) - (int)floor((2.0*bmin-2)/m);

Выражение (int)floor(1.0*bmax/m) нельзя переписать в виде bmax/m, так как при делении отрицательного числа на положительное округление компилятором C производится в большую сторону. А по условию задачи необходимо брать целую часть от числа (округление вниз). То есть при bmax < 0 приведенные выражения будут давать разные значения.

Умножаем res на amax – amin + 1 и печатаем результат:

res = res * (amax - amin + 1);

printf("Case %d: %d\n",i+1,res);