1563. Send a table
Jimmy have to calculate a
function f(x,
y) where x and y are both integers
in the range [1, n]. When he
knows f(x,
y), he can easily derive f(k*x,
k*y), where k is any integer from it by applying some simple calculations
involving f(x,
y) and k.
Note that the function f is not symmetric, so f(x, y) can not be derived from f(y, x).
For example if n = 4, he only needs to know the answers
for 11 out of the 16 possible input value combinations:

The other 5 can be derived from
them:
·
f(2, 2), f(3, 3) and f(4, 4) from f(1, 1);
·
f(2, 4) from f(1, 2);
·
f(4, 2) from f(2, 1);
Input. Consists of at most 600
lines. Each line
contains an integer n
(1
≤ n
≤ 50000). The last line contains
one zero and should not be processed.
Output. For each input value of n
print in a
separate line the minimum number of function values Jimmy needs to know to
compute all n2 values f(x, y).
|
Sample input |
Sample output |
245
0 |
311
19 |
SOLUTION
number theory – Euler’s function
Algorithm analysis
Let res(i) be the minimum required number of known values of f(x, y), where x, y Î {1, …, i}. Obviously, res(1) = 1, since for n = 1 it
is enough to know f(1, 1).
Let the value of res(i) is known. For n = i + 1 we must find the values
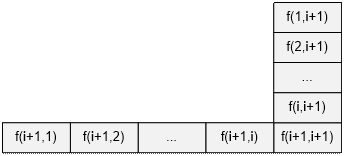
The values f(j, i + 1) and f(i + 1, j), j Î {1, …, i + 1} can be derived from the known values if GCD(j, i
+ 1) > 1, that is, if
the numbers j and i + 1
are not coprime. Therefore,
it is necessary to know all such f(j, i
+ 1) and f(i + 1, j), for which j and i + 1
are coprime. The
number of such values is 2 * j(i + 1), where j is Euler's
function. Thus
res(1) =
1,
res(i + 1) = res(i) + 2 * j(i + 1), i > 1
Example
Find the values of res(i) for some values of i:
res(1) =
1,
res(2) =
res(1) + 2 * j(2) = 1 + 2 * 1 = 3,
res(3) =
res(2) + 2 * j(3) = 3 + 2 * 2 = 7,
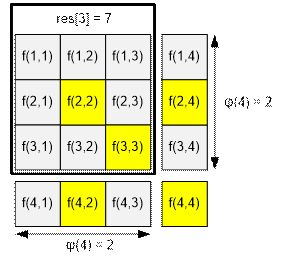
res(4) =
res(3) + 2 * j(4) = 7 + 2 * 2 = 11
Algorithm realization
The elements of array
f[i] of length MAX = 50001 will
contain the values j(i). The cells res[i]
will store the minimum required number of known values of f(x, y).
#define MAX 50001
int f[MAX], res[MAX];
Function fi finds the value of the Euler
function j(n).
int
fi(int n)
{
int i, result
= n;
for(i = 2; i
<= sqrt(n); i++)
{
if (n % i
== 0) result -= result / i;
while (n %
i == 0) n /= i;
}
if (n > 1)
result -= result / n;
return
result;
}
The main part of
the program. Find all values j(n), store them in f array.
f[1] = 0;
for(i = 2; i < MAX; i++) f[i] =
fi(i);
Set res[1] = 1 and
recursively recalculate the values of res[i].
res[1] = 1;
for(i = 2; i < MAX; i++) res[i] =
res[i-1] + 2 * f[i];
For each input
value of n output the
result res[n].
while(scanf("%d",&n),n)
printf("%d\n",res[n]);
Java realization
import java.util.Scanner;
public class Main
{
static int MAX = 50001;
static int fi(int n)
{
int result = n;
for(int i = 2 ; i <= Math.sqrt(n);i++)
{
if (n % i == 0) result -= result / i;
while (n % i == 0) n /= i;
}
if (n > 1) result -= result / n;
return result;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int f[] = new int[MAX];
int res[] = new int[MAX];
f[1] = 0;
for(int i = 2; i < MAX; i++)
f[i] = fi(i);
res[1] = 1;
for(int i = 2; i < MAX; i++)
res[i] = res[i-1] + 2 * f[i];
while(con.hasNext())
{
int n = con.nextInt();
if (n == 0) break;
System.out.println(res[n]);
}
con.close();
}
}