1568. Произведение троек

 

Заданы шесть целых чисел minx, maxx, miny, maxy, minz и maxz. Вычислить количество троек (x, y, z), которые удовлетворяют следующим условиям:

·        x находится между minx и maxx включительно

·        y находится между miny и maxy включительно

·        z находится между minz и maxz включительно

·        x * y = z

 

Вход.  Каждая строка содержит шесть целых чисел minx, maxx, miny, maxy, minz и maxz. Известно, что 1 ≤ maxx, maxy, maxz ≤ 109, 1 ≤ minx ≤ maxx, 1 ≤ miny ≤ maxy, 1 ≤ minz ≤ maxz.

 

Выход. Для каждой шестерки входных чисел вывести в отдельной строке количество троек (x, y, z), удовлетворяющих перечисленным выше условиям.

 

Пример входа

Пример выхода

2 2 3 3 6 6

6 8 4 5 27 35

8176 184561 1348 43168 45814517 957843164

1

4

2365846085

 

 

РЕШЕНИЕ

математика

 

Анализ алгоритма

Рассмотрим частный случай задачи. Пусть значение x0 фиксировано. Вычислим количество троек (x0, y, z), для которых

miny ≤ y ≤ maxy, minz ≤ z ≤ maxz и x0 * y = z

Выведем ограничения на y:

minz ≤ x0 * y ≤ maxz, minz / x0 ≤ y ≤ maxz / x0,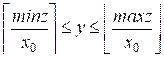

Объединим последнее ограничение на y с miny ≤ y ≤ maxy, получим:

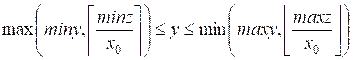
Поскольку любое целое значение y из указанного интервала порождает искомую тройку (x0, y, z), то количество последних при фиксированном x0 равно

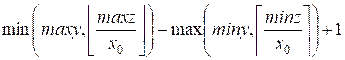
при условии, что указанная разница неотрицательна (иначе интервал y пуст).

Остается перебрать все значения minx ≤ x0 ≤ maxx и подсчитать количество троек для каждого из них. Однако такое решение не пройдет по времени.

 

Решения уравнения x * y = z будем искать отдельно для каждого из следующих случаев:

·        x = y = ; (1)

·         и таким образом ; (2)

·         и таким образом ; (3)

Тройки решений (x, y, z) во всех трех случаях не пересекаются.

Количество троек, для которых выполняется (1), равно количеству чисел из интервала [minx, maxx] ∩ [miny, maxy], не меньших  и не больших .

Для нахождения троек, удовлетворяющих (2), будем следовать выше описанному алгоритму, только перебор по x0 будем делать не только от minx до maxx, а еще и с условием . То есть minx ≤ x0 ≤ min (maxx, ).

Аналогично при нахождении троек, удовлетворяющих (3), будем совершать перебор y0 так, что miny ≤ y0 ≤ min (maxy, ).

 

Реализация алгоритма

Для заданного фиксированного значения x0 вычисляем количество троек (x0, y, z), удовлетворяющих условию задачи.

 

long long f(long long x0, long long miny, long long maxy,

                          long long minz, long long maxz)

{

 

Поскольку , то  или .

 

  minz = max(minz, x0 * x0 + 1);

  if (maxz < minz) return 0;

 

Вычисляем и возвращаем значение

.

 

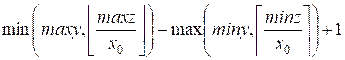  miny = max(miny, (minz + x0 - 1) / x0);

  maxy = min(maxy, maxz / x0);

  return max(0LL, maxy - miny + 1);

}

 

long long countTriplets(int minx, int maxx, int miny, int maxy,

                                  int minz, int maxz)

{

  long long x0, y0, i, res = 0;

 

Вычисляем количество троек (x, y, z), удовлетворяющих неравенству .

 

  for(x0 = minx; (x0 <= maxx) && (x0 * x0 < maxz); x0++)

    res += f(x0,miny,maxy,minz,maxz);

 

Вычисляем количество троек (x, y, z), удовлетворяющих неравенству , или то же самое что .

 

  for(y0 = miny; (y0 <= maxy) && (y0 * y0 < maxz); y0++)

    res += f(y0,minx,maxx,minz,maxz);

 

Вычисляем количество троек (x, y, z), удовлетворяющих равенству x = y = .

 

  for(i = max(minx,miny);(i <= min(maxx,maxy)) && (i*i <= maxz); i++)

    if (minz <= i * i) res ++;

  return res;

}

 

Основная часть программы.

 

while(scanf("%d %d %d %d %d %d",

            &minx,&maxx,&miny,&maxy,&minz,&maxz) == 6)

{

  res = countTriplets(minx,maxx,miny,maxy,minz,maxz);

  printf("%lld\n",res);

}