1569. Делители
Определим
функцию f(x), равную количеству
делителей числа x. По заданным двум
целым числам a и b (a £ b) вычислите f(a) + f(a + 1) + … + f(b).
Вход. Каждая строка содержит два целых числа a и b
(1 £ a £ b £ 231
– 1). Последняя строка содержит a = b = 0 и не обрабатывается.
Выход. Для каждой
входной пары чисел a и b выведите f(a) + f(a + 1) + … + f(b).
|
Пример
входа |
Пример
выхода |
|
9 12 1 2147483647 0 0 |
15 46475828386 |
РЕШЕНИЕ
математика
Анализ алгоритма
Обозначим через g(n)
= 
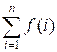сумму количества всех
делителей чисел от 1 до n. Ответом на
задачу будет значение f(a) + f(a + 1) + … + f(b) = g(b) – g(a – 1). Среди делителей чисел от 1 до n единица будет встречаться 
раз, двойка 
раз и так далее
(делитель i будет встречаться 
раз). То есть
g(n)
= 
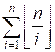
Поскольку n £ 231
– 1, то при вычислении g(n) получим
Time Limit. Распишем g(n) в виде двух
сумм:
g(n)
= 
+ 
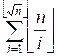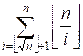
Первая сумма вычисляется в цикле за время 
.
Выражение 
при i от
до n принимает значения от 1 до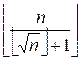 
. Рассмотрим, например, для скольких значений i имеет место равенство 
= k, где k
– натуральное число. Имеем: k ≤ n / i < k + 1. Откуда имеем два
неравенства:
·
i * k ≤ n или i ≤ n / k;
·
n < i * (k + 1) или i > n / (k
+ 1);
Откуда = k для всех i из интервала [n / (k + 1)
+ 1; n / k]. Количество таких целых i равно n / k – n / (k + 1). Следовательно
g(n)
= + = + 
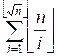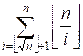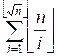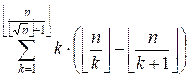
Например, принимает значение 1
для всех i от 
+ 1 до n. То есть при 
+ 1 ≤ i ≤ 
.
Пример
Пусть n = 12.
Рассмотрим таблицу значений , i = 1, 2, …, 12:
Найдем значение
выражения
g(12) =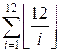 
= 
+ 
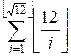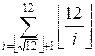
Учитывая, что 
, первая сумма равна
A = 12 / 1 + 12 /
2 + 12 / 3 = 12 + 6 + 4 = 22
При подсчете
второй суммы заметим, что:
·
= 1 для i из интервала от
+ 1 = 7 до 
= 12 (интервал [7; 12], всего 12/1 –
12/2 = 6 значений).
·
= 2 для i из интервала от
+ 1 = 5 до 
= 6 (интервал [5; 6], всего 12/2 –
12/3 = 2 значения).
·
= 3 для i из интервала от
+ 1 = 4 до 
= 4 (интервал [4; 4], всего 12/3 –
12/4 = 1 значение).
Вторая сумма
равна B = 1 * 6 + 2 * 2 + 3 * 1 = 6 + 4 + 3 = 13.
Следовательно
g(12) = 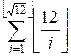+ 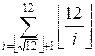= A + B = 22 + 13 = 35
Реализация
алгоритма
Реализация
функции g(n).
long long
g(long long n)
{
long long i, up, res = 0;
В следующем цикле вычисляем сумму .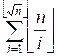
for(i = 1; i
<= (long long)sqrt(n);
i++)
res += n / i;
Присвоим up =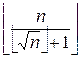 
.
up = n / ((long
long)sqrt(n) + 1);
Вычисляем сумму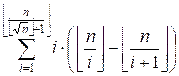 
.
for(i = 1; i
<= up; i++)
res += i * (n / i - n / (i + 1));
return res;
}
Основная часть программы.
while(scanf("%lld
%lld",&a,&b), a + b)
printf("%lld\n",g(b)
- g(a-1));
Java реализация
import java.util.*;
public class Main
{
static long g(long n)
{
long up, res = 0;
for(int i = 1; i <= (long)Math.sqrt(n); i++)
res += n / i;
up = n / ((long)Math.sqrt(n) + 1);
for(int i = 1; i <= up; i++)
res += i * (n / i - n / (i + 1));
return res;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
while(true)
{
long a = con.nextLong(), b = con.nextLong();
if (a + b == 0) break;
long res = g(b) - g(a-1);
System.out.println(res);
}
}
}