1569. Divisors
Define the function f(x) that equals to the number of divisors
of x. Given two integers a and b (a ≤ b), calculate the sum f(a) + f(a + 1) + … + f(b).
Input. Each line contains two integers a and b (1 £ a £ b £ 231 – 1). The
input is terminated by a line with a
= b = 0.
Output. For each test case print
in a separate line the value of f(a)
+ f(a + 1) + … + f(b).
|
Sample
input |
Sample
output |
|
9 12 1 2147483647 0 0 |
15 46475828386 |
SOLUTION
mathematics
Algorithm analysis
Let g(n) = ![]() be the sum of number
of divisors for all numbers from 1 to n.
The answer to the problem is the value f(a)
+ f(a + 1) + … + f(b) = g(b) – g(a – 1). Among the
divisors of numbers from 1 to n, one
appears
be the sum of number
of divisors for all numbers from 1 to n.
The answer to the problem is the value f(a)
+ f(a + 1) + … + f(b) = g(b) – g(a – 1). Among the
divisors of numbers from 1 to n, one
appears ![]() times, two
appears
times, two
appears ![]() times and so on (the
divisor i appears
times and so on (the
divisor i appears ![]() times). So
times). So
g(n)
= ![]()
Since n £ 231 – 1, then in the computing
of g(n) we get Time Limit. Write g(n) in the form of two sums:
g(n)
= 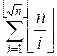 +
+ 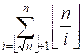
The first sum is calculated in a loop for ![]() .
.
The expression ![]() for i from
for i from ![]() to n takes values from 1 to
to n takes values from 1 to 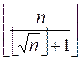 .
.
Let's consider, for example, for how many values of i the equality ![]() = k holds, where
k is a positive integer. We have: k ≤ n / i < k
+ 1. Whence we have two inequalities:
= k holds, where
k is a positive integer. We have: k ≤ n / i < k
+ 1. Whence we have two inequalities:
·
i * k ≤ n or i ≤ n / k;
·
n < i * (k + 1) or i > n / (k
+ 1);
Whence ![]() = k for all i from the
interval [n
/ (k + 1) + 1; n / k]. The count of such integers i is equal to n / k – n / (k + 1). Hence
= k for all i from the
interval [n
/ (k + 1) + 1; n / k]. The count of such integers i is equal to n / k – n / (k + 1). Hence
g(n)
= 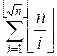 +
+ 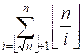 =
= 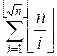 +
+ 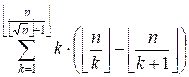
For example, ![]() takes the value 1 for
all i from
takes the value 1 for
all i from ![]() + 1 to n. That is, when
+ 1 to n. That is, when ![]() + 1 ≤ i ≤
+ 1 ≤ i ≤ ![]() .
.
Example
Let n = 12. Consider the following
table of ![]() (i = 1, 2, …, 12) values:
(i = 1, 2, …, 12) values:

Let's find the
value of the expression
g(12) = 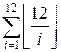 =
= 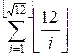 +
+ 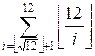
Taking into account that ![]() , the first sum equals to
, the first sum equals to
A = 12/1 + 12/2 + 12/3 =
12 + 6 + 4 = 22
Calculating the second
sum, we note that
·
![]() = 1 for i from interval from
= 1 for i from interval from ![]() + 1 = 7 to
+ 1 = 7 to ![]() = 12 (interval [7; 12], in total 12/1 –
12/2 = 6 values).
= 12 (interval [7; 12], in total 12/1 –
12/2 = 6 values).
·
![]() = 2 for i from interval
from
= 2 for i from interval
from ![]() + 1 = 5 to
+ 1 = 5 to ![]() = 6 (interval [5; 6], in total 12/2 –
12/3 = 2 values).
= 6 (interval [5; 6], in total 12/2 –
12/3 = 2 values).
·
![]() = 3 for i from interval
from
= 3 for i from interval
from ![]() + 1 = 4 to
+ 1 = 4 to ![]() = 4 (interval [4; 4], in total 12/3 –
12/4 = 1 value).
= 4 (interval [4; 4], in total 12/3 –
12/4 = 1 value).
The second sum equals to B
= 1 * 6 + 2 * 2 + 3 * 1 = 6 + 4 + 3 = 13.
Hence
g(12) = 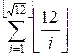 +
+ 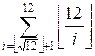 = A + B = 22 + 13 = 35
= A + B = 22 + 13 = 35
Algorithm realization
Implementation of function
g(n).
long long g(long long n)
{
long long
i, up, res = 0;
In the next loop we evaluate the sum ![]() .
.
for(i = 1; i <= (long long)sqrt(n);
i++)
res += n / i;
Assign up = 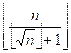 .
.
up = n / ((long long)sqrt(n)
+ 1);
Calculate the sum 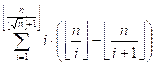 .
.
for(i = 1; i <= up; i++)
res += i * (n / i - n / (i + 1));
return res;
}
The main part of the program.
while(scanf("%lld %lld",&a,&b),
a + b)
printf("%lld\n",g(b) -
g(a-1));