1575. Боже! Спаси меня

Вы находитесь в комнате с n дверями. Если открыть дверь с номером i, то через x_i часов Вы либо попадете в безопасное место, либо снова вернетесь в эту же комнату. Вычислите ожидаемое время P (в часах), через которое Вы сможете выбраться из комнаты в безопасное место.

Вход. Первая строка содержит количество тестов. Первая строка каждого теста содержит количество дверей n (0 < n < 100). Каждая из следующих n строк содержит два числа x_i (0 < | x_i | < 25) и p_i (0 ≤ p_i ≤ 1).

· если x_i  положительно, то оно обозначает время, через которое Вы сможете попасть в безопасное место;

· если x_i отрицательно, то | x_i | обозначает время, через которое Вы снова окажетесь в комнате;

Здесь p_i – вероятность открытия i - ой двери. Сумма всех p_i равна 1.

Выход. Для каждого теста выведите его номер, двоеточие, пробел и затем:

· фразу “God! Save me”, если выбраться из комнаты невозможно;

· либо ожидаемое время P с 6 десятичными знаками, через которое можно выбраться из комнаты в безопасное место.

Пример входа	Пример выхода
3 3 2 0.33 -3 0.33 -5 0.34 3 2 0.34 -3 0.33 -5 0.33 3 10 0.0 -1 0.4 -1 0.6	Case 1: 10.151515 Case 2: 9.764706 Case 3: God! Save me

РЕШЕНИЕ

вероятность + математика

Анализ алгоритма

Обозначим через P ожидаемое время, через которое можно выбраться из комнаты в безопасное место. Тогда это время выражается следующим образом:

P = ,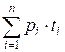

где t_i – время выхода в безопасное место, если выбрать i – ую дверь. Очевидно, что t_i = x_i, если x_i > 0. Если x_i < 0, то для того чтобы выбраться, нужно сначала потратить время -x_i на возвращение в комнату, а затам время P на повторную попытку выхода. Таким образом, в этом случае t_i = -x_i + P.

В результате получаем линейное уравнение относительно P. Построить и решить это уравнение можно за время O(n), где n – количество дверей.

Пример

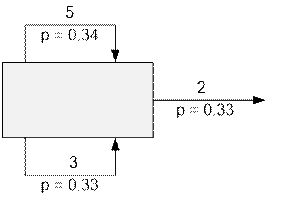
Рассмотрим первый тест. Составим уравнение:

P = 0.33 * 2 + 0.33 * (3 + P) + 0.34 * (5 + P),

откуда 0.33 * P = 3.35 или P = 10.151515.

Реализация алгоритма

Решение линейного уравнения будем проводить следующим образом. Все слагаемые, содержащие множитель P, перенесем влево, а их коэффициенты будем хранить в переменной left. Все константы соберем справа и сохраним в переменной right. Изначально установим left = 1 и right = 0.

Читаем n пар чисел x и p.

· Если x > 0, то увеличиваем правую часть уравнения на величину x * p.

· Если x < 0, то в правой части уравнения появится слагаемое p * (-x + P). В этом случае следует прибавить к правой части величину p * (-x), а из левой вычесть p.

left = 1.0; right = 0.0;

scanf("%d",&n);

for(j = 0; j < n; j++)

{

scanf("%lf %lf",&x, &p);

if (x < 0.0)

{

left -= p;

right += p * (-x);

} else

right += x * p;

}

Получили уравнение left * P = right. Если left = 0, то выбраться из комнаты невозможно (не существует двери, ведущей в безопасное место). В противном случае искомое время можно вычислить как P = right / left.

if (left > 0.0)

{

res = right / left;

Выводим ответ. Переменной i соответствует номер теста.

printf("Case %d: %.2lf\n",i,res);

} else

printf("Case %d: God! Save me\n",i);