1575. God! Save me

You are in a room with n doors. If you open the door numbered i, then after x_i hours you will either reach a safe place or return to this same room. Calculate the expected time P (in hours) after which you can escape the room to a safe place.

Input. The first line contains the number of tests. The first line of each test contains the number of doors n (0 < n < 100). Each of the following n lines contains two numbers x_i (0 < | x_i | < 25) and p_i (0 ≤ p_i ≤ 1).

· If x_i is positive, it represents the time after which you can reach a safe place;

· If x_i is negative, then ∣x_i∣ represents the time after which you will find yourself back in the room;

Here, p_i is the probability of opening the i-th door. The sum of all p_i equals 1.

Output. For each test, print its number, a colon, a space, and then:

· the phrase “God! Save me” if it is impossible to escape from the room;

· or the expected time P with 6 decimal places, after which you can escape from the room to a safe place.

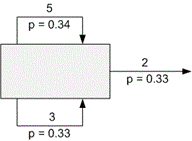
Sample input	Sample output
3 3 2 0.33 -3 0.33 -5 0.34 3 2 0.34 -3 0.33 -5 0.33 3 10 0.0 -1 0.4 -1 0.6	Case 1: 10.151515 Case 2: 9.764706 Case 3: God! Save me

SOLUTION

probability

Algorithm analysis

Let P denote the expected time to escape the room to a safe place. This time is expressed as follows:

P = ,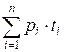

where t_i is the time to reach a safe place if the i-th door is chosen. It is clear that t_i = x_i if x_i > 0. If x_i < 0, then to escape, one must first spend time -x_i to return to the room, and then spend time P for another attempt to exit. Thus, in this case, t_i = -x_i + P.

As a result, we obtain a linear equation in terms of P. This equation can be constructed and solved in O(n) time, where n is the number of doors.

Example

Let’s consider the first test. Create an equation:

P = 0.33 * 2 + 0.33 * (3 + P) + 0.34 * (5 + P),

where from 0.33 * P = 3.35 or P = 10.151515.

Algorithm realization

We’ll solve the linear equation as follows. All terms containing the multiplier P will be moved to the left side, and their coefficients will be stored in the variable left. All constants will be collected on the right side and stored in the variable right. Initially, set left = 1 and right = 0.

Read n pairs of numbers x and p.

· If x > 0, then increase the right side of the equation by x * p.

· If x < 0, a term p * (-x + P) will appear on the right side of the equation. In this case, we should add p * (-x) to the right side and subtract p from the left side.

left = 1.0; right = 0.0;

scanf("%d",&n);

for(j = 0; j < n; j++)

{

scanf("%lf %lf",&x, &p);

if (x < 0.0)

{

left -= p;

right += p * (-x);

} else

right += x * p;

}

We obtained the equation left * P = right. If left = 0, then it is impossible to escape from the room (there is no door leading to a safe place). Otherwise, the sought time can be calculated as P = right / left.

if (left > 0.0)

{

res = right / left;

Print the answer. The variable i corresponds to the test number.

printf("Case %d: %.2lf\n",i,res);

} else

printf("Case %d: God! Save me\n",i);