1579. Тройной прыжок

Тройной прыжок совершается следующим образом. Прыгун разгоняется, добегает до определенной отметки и совершает три последовательных прыжка. Победителем является тот, чья суммарная длина прыжков наибольшая.

Вы принимаете участие в соревновании и прыгаете последним. Все Ваши соперники уже совершили прыжки, поэтому их результаты известны.

Первый свой прыжок Вы уже совершили, его длина равна first. Длина каждого из оставшихся прыжков может с одинаковой вероятностью принимать любое значение из отрезка [lower, upper], и не обязательно быть целым. Вам необходимо вычислить вероятность того, что Вы займете i - ое место. Место, занятое Вами, равняется единице плюс количество соперников, которые прыгнули дальше Вас.

Вход. Состоит из нескольких тестов. Первая строка каждого теста содержит значения lower, upper, first (1 ≤ lower ≤ 1000, lower ≤ upper ≤ 1000, lower ≤ first ≤ upper) и количество Ваших соперников n (1 ≤ n ≤ 50). Вторая строка теста содержит n целых чисел от 1 до 3000 – длины тройных прыжков всех Ваших соперников.

Выход. Для каждого теста в отдельной строке вывести n + 1 действительных чисел – соответственно вероятности того что Вы займете первое, второе, третье, ..., последнее место. Все вероятности следует выводить с 4 десятичными знаками.

Пример входа

1 2 1 4

1 2 3 4

1 10 5 8

1 2 3 5 10 11 12 19

Пример выхода

0.5000 0.5000 0.0000 0.0000 0.0000

0.2222 0.6235 0.0556 0.0432 0.0556 0.0000 0.0000 0.0000 0.0000

РЕШЕНИЕ

вероятность

Анализ алгоритма

Отнимем величину первого прыжка от всех результатов прыжков соперников, таким образом сведя задачу к “двойному” прыжку. Из условия задачи следует, что длина каждого прыжка является независимой случайной величиной, равномерно распределенной на отрезке [lower, upper]. Сумма двух прыжков также является случайной величиной, определенной на отрезке [2*lower, 2*upper]. Но она уже не будет равномерно распределенной.

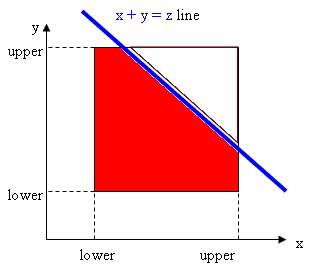
Определим случайную величину F(z) = {сумма двух прыжков не более z}. F(z) пропорционально площади области квадрата под прямой z = x + y, изображенной красным цветом.

Функция распределения F(z) имеет вид:

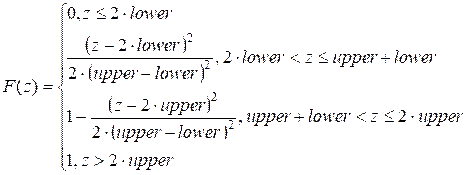
Отсортируем длины прыжков соперников по убыванию. Вероятность занять первое место равна 1 – F(opponents[0]). Вероятность занять второе место равна F(opponents[0]) – F(opponents[1]) и так далее. Вероятность занять последнее место равна F(opponents[n – 1]), где n – количество соперников.

Реализация алгоритма

Реализация функции распределения F(z).

double f(double lower, double upper, double z)

{

if (z <= 2 * lower) return 0.0;

if (z <= lower + upper) return (z – 2 * lower) * (z - 2*lower) / 2 /

(upper-lower) / (upper - lower);

if (z <= 2 * upper)

return 1 - (z – 2 * upper) * (z – 2 * upper) / 2 /

(upper-lower) / (upper - lower);

return 1.0;

}

Искомые вероятности заносим в массив res. Отдельно вычисляем значения res[0] и res[n].

void getProbabilities(int lower, int upper, int first)

{

int i;

for(i = 0; i < n; i++) opponents[i] -= first;

sort(opponents,opponents+n,greater<int>());

res[0] = 1 - f(lower,upper,opponents[0]);

res[n] = f(lower,upper,opponents[n-1]);

for(i = 1; i < n; i++)

res[i] = f(lower,upper,opponents[i-1]) –

f(lower,upper,opponents[i]);

}

Основная часть программы.

while(scanf("%d %d %d %d",&lower,&upper,&first,&n) == 4)

{

for(i = 0; i < n; i++) scanf("%d",&opponents[i]);

getProbabilities(lower, upper, first);

for(i = 0; i < n + 1; i++) printf("%.4lf ",res[i]); printf("\n");

}