1585. Игра в лотерею
Возвращаясь
домой, Вы заметили объявление:
“Выберите m различных чисел в диапазоне от 1 до n включительно. Мы случайным образом выберем m различных чисел в том же
диапазоне. Если хотя бы k чисел совпадут, Вы выиграете”.
Вычислите
вероятность Вашего выигрыша.
Вход. Каждая строка
является отдельным тестом и содержит три целых числа n, m и k (2 ≤ n ≤ 8, 1 ≤ m ≤ n – 1, 1 ≤ k ≤ m).
Выход. Для каждого теста в отдельной строке выведите вероятность
Вашего выигрыша с не менее 4 десятичными знаками.
|
Пример
входа |
Пример
выхода |
|
3 2 1 8 2 1 8 4 2 |
1.0000 0.4643 0.7571 |
РЕШЕНИЕ
теория вероятности
Анализ алгоритма
Рассмотрим
случай, когда следует угадать 5 номеров из 39. Очевидно, что вероятность угадать
все 5 номеров составит ![]() . Теперь вычислим вероятность того, что будет угадано в точности 4
номера. В этом случае из 5 номеров, выбранных игроком, 4 должны совпасть с 5 выпавших
номерами (
. Теперь вычислим вероятность того, что будет угадано в точности 4
номера. В этом случае из 5 номеров, выбранных игроком, 4 должны совпасть с 5 выпавших
номерами (![]() вариантов), а один оставшийся номер должен быть среди 39 – 5 = 34 невыпавших
(
вариантов), а один оставшийся номер должен быть среди 39 – 5 = 34 невыпавших
(![]() вариантов).
вариантов).
В общем случае, для того чтобы угадать
ровно x номеров,
необходимо чтобы эти x номеров
находились среди m выпавших, а
остальные m – x номеров находились среди n
– m невыпавших. Вероятность угадать в
точности x номеров равна
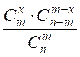
Для нахождения
искомой вероятности необходимо просуммировать вероятности угадывания ровно x номеров для каждого x от k до m
включительно.
Реализация алгоритма
Функция Cnk вычисляет значение биномиального коэффициента ![]() .
.
int Cnk(int
k, int n)
{
long long res = 1;
if (k > n)
return 0;
if (k > n
- k) k = n - k;
for (int i = 1; i <= k; i++)
res = res * (n - i + 1) / i;
return (int)res;
}
Основная часть программы. Вычисляем
результат, равный
res = 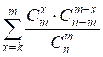 =
= 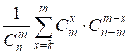
while(scanf("%d
%d %d",&n,&m,&k) == 3)
{
for (res = 0,
x = k; x <= m; x++)
res += Cnk(x,m) * Cnk(m-x,n-m);
res = res / Cnk(m,n);
printf("%.4lf\n",res);
}