1592. Мост
n человек
подошли ночью к реке. Имеется узкий мост, который одновременно может вместить
только двух человек. У них есть один фонарик, и, поскольку сейчас ночь, при
переходе через мост его необходимо использовать. Движение по мосту без фонаря
запрещено.
Для каждого человека известно время, за которое он
пересекает мост. Если по мосту двигаются двое, то время их передвижения равно
времени более медленного. Необходимо найти минимальное время, за которое все n людей
перейдут на другой берег реки, а также последовательность переходов, как
указано в примере.
Вход. Состоит из
нескольких тестов. Первая строка каждого теста содержит количество людей n (n
£ 1000), а вторая строка содержит n чисел
– время перехода людей через мост. Время перехода каждого человека через мост не более 100
секунд.
Выход. Для каждого
теста вывести следующую информацию. Первая строка содержит минимальное время,
за которое могут пересечь мост n
людей. Далее следует стратегия пересечения моста людьми. Каждая строка
стратегии содержит одно или два числа, характеризующие людей, которые с фонарем
пересекают мост. При существовании нескольких оптимальных стратегий пересечения
реки вывести любую.
|
Пример входа |
Пример выхода |
|
4 1 2 5 10 3 1 2 3 |
17 1 2 1 5 10 2 1 2 6 1 2 1 1 3 |
РЕШЕНИЕ
жадный
алгоритм
Анализ алгоритма
Отсортируем время, за которое люди
пересекают реку, по возрастанию. Обозначим через ti время пересечения реки i – ым человеком (t1 £ t2 £ … £ tn). Рассмотрим, как
следует пересекать мост одному, двум или трем людям. При n = 1 и n = 2 оптимальная
скорость пересечения реки соответственно равна t1 и t2 = max(t1, t2) (скорость передвижения двух людей равна скорости медленного). При наличии
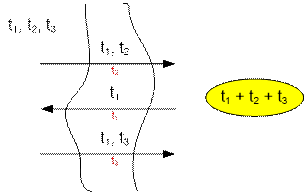
трех людей (n = 3) первый и второй
перебираются на другую сторону, самый быстрый (первый) возвращается с фонарем
назад и переводит третьего. Таким образом, оптимальное время перехода равно t1 + t2 + t3.
Рассмотрим случай, когда n > 3. Пусть A £ B £ … £ Y £ Z – люди, отсортированные по возрастанию времени пересечения
моста (A – самый быстрый, Z – самый медленный). Пусть J – это человек, с
которым перемещается Z. Если J остается на другом берегу и никогда больше не
пойдет по мосту, то оптимально выбрать его равным Y. Если J будет возвращаться, то его оптимально
выбрать самым быстрым, то есть А. Таким образом Z может пересекать мост или с
Y, или с А.

Вычислим время перевода двух самых медленных людей (Y и Z)
согласно этим двум стратегиям.
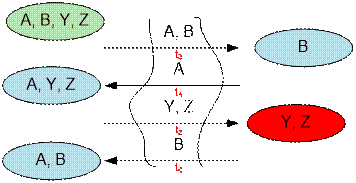
1. Z идет с Y. Но тогда до этого там должен быть кто-то,
кто вернет фонарь, например K. Но этого K также на другой берег должен был
кто-то провести чтобы, вернув фонарь, отдать его Y и Z. Пусть им будет L. Таким
образом, K и L должны возвращаться. Для минимизации времени в качестве K и L
следует выбрать двух самых быстрых, то
есть A и B. Время перевода Y и Z равно tA + 2tB + tZ.
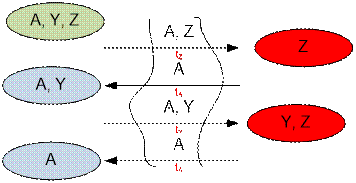
2. Z пересекает мост с A, A возвращается. Далее A
переводит Y и также возвращается. Время, за которое Y и Z перейдут на другой
берег, равно 2tA + tY + tZ.
В обоих случаях через мост переводятся только двое самых
медленных людей. Стратегия (первая или вторая) выбирается в зависимости от
того, какое из значений (tA + 2tB + tZ или 2tA + tY + tZ) меньше. Если изначально следовало перевести n людей, то далее рекурсивно следует
перевести n – 2 людей.
Пример
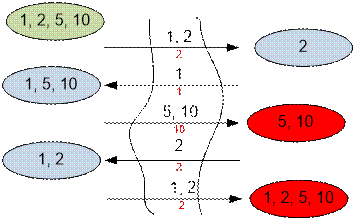
Отсортируем время пересечения моста людьми: 1, 2, 5, 10.
Здесь tA = 1, tB = 2, tY = 5, tZ = 10. Время перевода двух самых медленных людей согласно
первой и второй стратегиям соответственно равны
·
tA + 2tB + tZ = 1 + 2 * 2 + 10 = 15;
·
2tA + tY + tZ = 2 * 1 + 5 + 10 = 17;
Поскольку первое значение меньше, то следует Z вести с Y.
Z с Y пересекут мост за время 15, после чего остается перевести на другой берег
A и B. Это делается за время max{tA, tB} = 2.
Общее время перехода моста равно 15 + 2 = 17.
Реализация алгоритма
В массиве m хранится время перехода людей через реку.
int m[1001];
Функция go(n, visible) возвращает оптимальное время,
за которое могут пересечь реку n
людей. Переменная visible = 1, если
следует выводить на экран саму стратегию перехода, и visible = 0 иначе.
int go(int n,int visible)
{
int First,
Second, Best;
Случай пересечения реки одним человеком.
if (n == 1)
{
if (visible)
printf("%d\n",m[0]);
return m[0];
} else
Случай пересечения реки двумя людьми
if (n == 2)
{
if (visible) printf("%d
%d\n",m[0],m[1]);
return m[1];
} else
Случай пересечения реки тремя людьми
if (n == 3)
{
if (visible)
{
printf("%d %d\n",m[0],m[1]);
printf("%d\n",m[0]);
printf("%d %d\n",m[0],m[2]);
}
return m[0] + m[1] + m[2];
};
Вычисляем оптимальное время First и Second, которое
получается при использовании двух выше описанных стратегий.
First = m[0] + 2 *
m[1] + m[n-1];
Second = 2 * m[0] +
m[n-2] + m[n-1];
Best = (First <
Second) ? First : Second;
if (visible)
{
if (Best == First)
{
printf("%d %d\n",m[0],m[1]);
printf("%d\n",m[0]);
printf("%d %d\n",m[n-2],m[n-1]);
printf("%d\n",m[1]);
} else
{
printf("%d %d\n",m[0],m[n-2]);
printf("%d\n",m[0]);
printf("%d %d\n",m[0],m[n-1]);
printf("%d\n",m[0]);
}
}
Рекурсивно вычисляем оптимальную стратегию для оставшихся n – 2 людей.
return Best + go(n-2,visible);
}
Основная часть программы. Читаем количество тестов, вводим
время, за которое люди пересекают мост в массив m.
while(scanf("%d",&n)
== 1)
{
for(i = 0; i
< n; i++) scanf("%d",&m[i]);
Сортируем время пересечения реки людьми по возрастанию.
sort(m,m+n);
Запускаем функцию go с параметром visible = 0, которая возвращает оптимальное время пересечения реки.
Выводим его, после чего снова запускаем функцию go с параметром visible = 1, которая печатает
последовательность переходов.
res = go(n,0);
printf("%d\n",res);
res = go(n,1);
}