1599. Динамическая лягушка

В связи с расширением использования пестицидов, местные ручьи и реки оказались настолько загрязненными, что стали почти невозможными для жизни водных животных.

Лягушка Фред находится на левом берегу такой реки. n камней расположено на прямой линии, простирающейся с левого берега на правый. Расстояние между левым и правым берегом d метров. Камни могут быть двух размеров: крупные могут выдержать любой вес, но мелкие начинают тонуть, как только на них окажется тело любой массы. Фреду нужно перейти на правый берег, где он должен собрать подарки и вернуться обратно на левый берег в свой дом.

Фрейд может приземлиться на каждый маленький камень не более чем один раз. Крупные может использовать столько раз, сколько пожелает. В воду он прыгнуть не может, так она чрезвычайно загрязнена.

Можете ли вы спланировать маршрут так, чтобы минимизировать максимальное расстояние одного прыжка?

Вход. Первая строка содержит количество тестов t (t < 100). Каждый тест начинается двумя целыми числами n (0 ≤ n ≤ 100) и d (1 ≤ d ≤ 10⁹). Следующая строка описывает n камней. Каждый камень задается в виде s-m. Симол s укзывает на тип камня – Большой (B) или Маленький (S), а m (0 < m < d) определяет расстояние от этого камня до левого берега. Камни задаются в порядке возрастания значений m.

Выход. Для каждого теста вывести его номер и минимально возможное значение наибольшего прыжка.

Пример входа 1	Пример выхода 1
3 1 10 B-5 1 10 S-5 2 10 B-3 S-6	Case 1: 5 Case 2: 10 Case 3: 7
Пример входа 2	Пример выхода 2
1 6 50 S-2 B-14 S-20 S-26 B-38 S-43	Case 1: 18

РЕШЕНИЕ

жадный алгоритм

Анализ алгоритма

Очевидно, что на обратном пути лягушка может использовать все имеющиеся у нее на пути камни. Нам необходимо разработать стратегию передвижения лягушки с левого берега на правый. Будем считать, что левый и правый берег являются большими камнями, и изначально лягушка находится на самом левом камне. Теперь каждый большой камень заменим на два маленьких, находящихся в одном и том же месте. Это можно сделать, так как очевидно, что лягушка будет использовать любой большой камень не более двух раз. Поскольку теперь у нас имеется последовательность только маленьких камней, то сформулируем алгоритм движения лягушки: при движении с левого на правый берег она должна каждый раз перепрыгивать через один камень – в этом и состоит принцип жадного подхода.

Пример

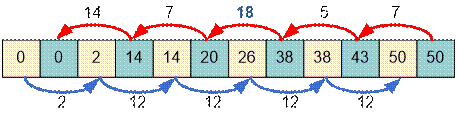
Рассмотрим второй тест. Переправа содержит n = 6 камней, расстояние между берегами d = 50. Левый и правый берег представляем большими камнями. Массив и движение лягушки по нем имеет следующий вид.

Реализация алгоритма

Читаем входные данные.

scanf("%d\n",&tests);

for(t = 1; t <= tests; t++)

{

scanf("%d %d\n",&n,&d);

memset(m,-1,sizeof(m));

Левый берег представляем одним большим камнем, который заменяем на два маленьких.

m[0] = m[1] = 0;

Считываем информацию про камни и заполняем массив m. Каждый большой камень заносим в массив дважды, маленький – только один раз.

for(ptr = 2, i = 0; i < n; i++)

{

do {scanf("%c",&letter);} while (letter == ' ');

scanf("-%d",&s);

if (letter == 'B') {m[ptr] = m[ptr+1] = s; ptr += 2;}

else {m[ptr] = s; ptr++;}

}

Правый берег представляем одним большим камнем, который заменяем на два маленьких.

m[ptr] = m[ptr+1] = d;

ptr++;

scanf("\n");

Движемся с самого левого камня до самого правого, перепрыгивая через один. Ищем максимум разностей между i-ым и (i + 2)-ым камнями.

for(dist = 0, i = 2; i < ptr; i += 2)

if (m[i] - m[i-2] > dist) dist = m[i] - m[i-2];

Уменьшаем значение i на 1. Теперь движемся справа налево по соседним камням, которые имеют нечетные номера (камни с четными номерами утонули при движении лягушки на правый берег).

for(i--; i >= 2; i -= 2)

if (m[i] - m[i-2] > dist) dist = m[i] - m[i-2];

Выводим ответ.

printf("Case %d: %d\n",t,dist);

}