1614. Angles of triangle

The triangle is given. Find the value of its biggest angle.

Input. The coordinates of triangle vertices are given. The coordinates of a vertex is a pair of integers not greater than 10⁴ by absolute value.

Output. Print the value of its biggest angle in degrees with accuracy no less than 6 decimal digits.

Sample input	Sample output
0 0 3 0 0 4	90.000000

SOLUTION

geometry

Algorithm analysis

First, find the lengths of the sides of triangle. Then use the cosine theorem

a² = b² + c² – 2 * b * c * cos ∠BAC

to compute its angles. It remains to find the largest of three angles.

The distance d_AB between points A(x₁, y₁) and B(x₂, y₂) is

d_AB =

Example

The triangle given in the problem statement has the form:

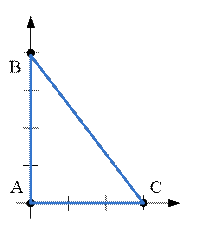
The largest angle of triangle is 90º.

Algorithm realization

The angles of triangle in degrees will be stored in the angles array.

double angles[3];

Read the coordinates of triangle’s vertices. Calculate the lengths of its sides a, b, c.

scanf("%d %d %d %d %d %d",&x_1,&y_1,&x_2,&y_2,&x_3,&y_3);

a = sqrt(1.0*(x_2 - x_1)*(x_2 - x_1) + (y_2 - y_1)*(y_2 - y_1));

b = sqrt(1.0*(x_2 - x_3)*(x_2 - x_3) + (y_2 - y_3)*(y_2 - y_3));

c = sqrt(1.0*(x_3 - x_1)*(x_3 - x_1) + (y_3 - y_1)*(y_3 - y_1));

Calculate the angles of a triangle using the cosine theorem. Convert angle values from radians to degrees.

angles[0] = acos((b*b + c*c - a*a) / (2*b*c)); angles[0] *= 180 / PI;

angles[1] = acos((a*a + b*b - c*c) / (2*a*b)); angles[1] *= 180 / PI;

angles[2] = acos((a*a + c*c - b*b) / (2*a*c)); angles[2] *= 180 / PI;

Find the value of the largest angle mx and print it.

for(mx = i = 0; i < 3; i++)

if (angles[i] > mx) mx = angles[i];

printf("%.6lf\n",mx);

Java realization

import java.util.*;

public class Main

{

static double angles[] = new double[3];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int x1 = con.nextInt(), y1 = con.nextInt();

int x2 = con.nextInt(), y2 = con.nextInt();

int x3 = con.nextInt(), y3 = con.nextInt();

double a = Math.sqrt((x2 - x1)*(x2 - x1) + (y2 - y1)*(y2 - y1));

double b = Math.sqrt((x2 - x3)*(x2 - x3) + (y2 - y3)*(y2 - y3));

double c = Math.sqrt((x3 - x1)*(x3 - x1) + (y3 - y1)*(y3 - y1));

angles[0] = Math.acos((b*b + c*c - a*a) / (2*b*c));

angles[0] *= 180 / Math.PI;

angles[1] = Math.acos((a*a + b*b - c*c) / (2*a*b));

angles[1] *= 180 / Math.PI;

angles[2] = Math.acos((a*a + c*c - b*b) / (2*a*c));

angles[2] *= 180 / Math.PI;

double max = 0;

for(int i = 0; i < 3; i++)

if (angles[i] > max) max = angles[i];

System.out.println(max);

con.close();

}

}

Python realization

import math

x1, y1 = map(float,input().split())

x2, y2 = map(float,input().split())

x3, y3 = map(float,input().split())

a = math.sqrt((x2 - x1)*(x2 - x1) + (y2 - y1)*(y2 - y1))

b = math.sqrt((x2 - x3)*(x2 - x3) + (y2 - y3)*(y2 - y3))

c = math.sqrt((x3 - x1)*(x3 - x1) + (y3 - y1)*(y3 - y1))

angles = [math.acos((b*b + c*c - a*a) / (2*b*c)),

math.acos((a*a + b*b - c*c) / (2*a*b)),

math.acos((a*a + c*c - b*b) / (2*a*c))]

angles = [x * 180 / math.pi for x in angles]

print("%.6f" %max(angles))