1618. The Longest Common Subsequence
Two sequences are
given. Find the length of their longest common subsequence.
A subsequence is
a sequence that can be derived from the original sequence by deleting some
elements without changing the order of the remaining elements.
Input. The first line
contains one integer n (1 ≤ n ≤ 1000) – the length of
the first sequence.
The second line
contains n integers – the elements of the first sequence, each of which
does not exceed 104 in absolute value.
The third line
contains one integer m (1 ≤ m ≤ 1000) – the length of
the second sequence.
The fourth line
contains m integers – the elements of the second sequence,
each of which does not exceed 104 in absolute value.
Output. Print one
integer – the length of the longest common subsequence of the two given
sequences.
|
Sample
input |
Sample
output |
|
3 1 2 3 4 2 1 3 5 |
2 |
SOLUTION
dynamic programming
longest common subsequence
Algorithm analysis
The subsequence
of a given sequence is a set of elements arranged in the same order as in the
original sequence but not necessarily contiguous. A subsequence can be obtained
from the original sequence by removing some of its elements.
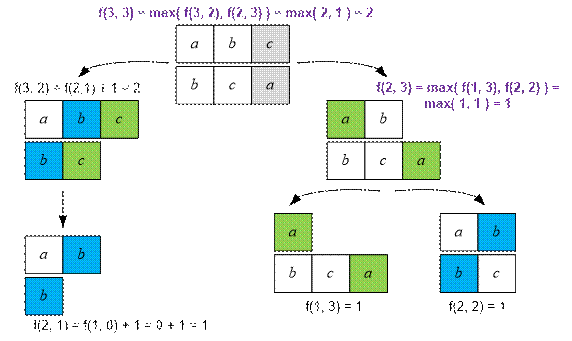
For example, consider the
sequence {2, 1, 3, 5}. Then
·
{1, 5}, {2}, {2, 3, 5} are subsequences;
·
{5, 1}, {2, 3, 1} are not subsequences;
The common
subsequence of two sequences is a subsequence that appears in both
sequences. The longest common subsequence (LCS) is a common subsequence
of maximum length.
For example, the longest common subsequence
of the sequences {1, 2, 3} and {2, 1, 3, 5} can be {1, 3} or {2, 3}. In this case, the
length of the LCS is 2.
Let f(i, j)
be the length
of the longest
common subsequence of the sequences x1x2…xi
and y1y2…yj.
If xi ¹ yj, the LCS should be found among two
options:
·
the prefixes x1x2…xi
and y1y2…yj-1 (their LCS is f(i, j
– 1)),
·
the prefixes x1x2…xi-1 and y1y2…yj
(their LCS is f(i – 1, j)).
Return the maximum of these values:
f(i, j) = max( f(i,
j – 1), f(i – 1, j) )

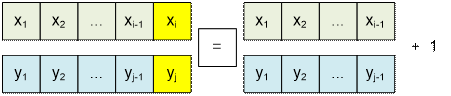
If xi = yj,
add the
current element xi to the LCS and consider the shorter
prefixes x1x2…xi-1 and y1y2…yj-1:
f(i, j) = 1 + f(i –
1, j – 1)
If one of the sequences is
empty, then their LCS is also empty:
f(0, j) = f(i, 0) = 0
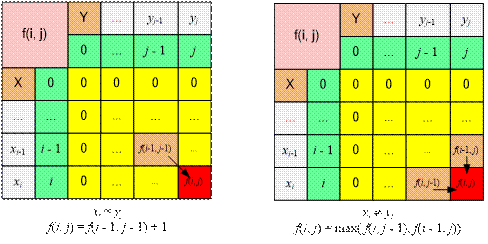
The recurrence relation
for computing the LCS length is as follows:
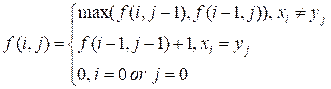
Let’s consider an
example of the
calculations:
The values of f(i, j)
will be
stored in an array m[0..1000, 0..1000], where m[0][i] = m[i][0]
= 0. Each
subsequent row of the array m[i][j] is computed based on the previous
one. Thus, to find the result, it is sufficient to store only two rows of
length 1000 in memory.
Example
Let X = abcdgh,
Y = aedfhr. The longest common subsequence is adh, and its length is f(6, 6) = 3.
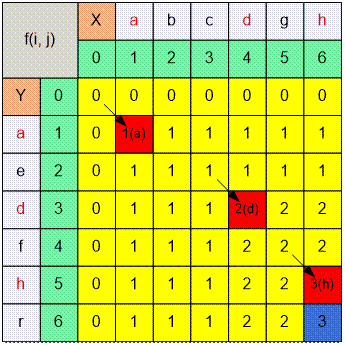
f(6, 6) = max(f(6, 5),
f(5, 6)) = max(2, 3) = 3, because Y[6] = r ≠ h = X[6].
f(5, 6) = 1 + f(4, 5) = 1
+ 2 = 3, because Y[5] = h = X[6].
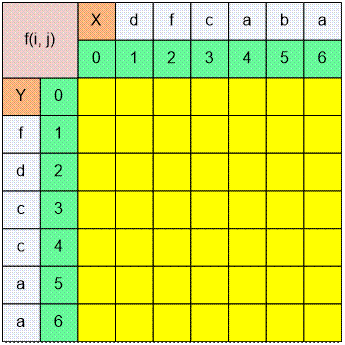
Exercise
Fill the following table:
Algorithm implementation
The arrays x and y contain the input
sequences, and n and m are their lengths. The array mas stores the last two rows
of dynamic computations.
#define SIZE 1010
int x[SIZE], y[SIZE], mas[2][SIZE];
Read the input sequences into
the arrays, starting
from the first index, i.e., into the cells x[1..n] and y[1..m].
scanf("%d",&n);
for (i = 1; i <=
n; i++) scanf("%d",&x[i]);
scanf("%d",&m);
for (i = 1; i <=
m; i++) scanf("%d",&y[i]);
Initialize the array mas with zeros.
memset(mas,0,sizeof(mas));
Compute the values of the function f(i, j).
Initially mas[0][j] contains the values f(0, j) = 0. Next, mas[1][j] is used to store the values f(1, j).
Since computing f(2, j) only
requires the values from the previous row of the mas array, the values
of f(2, j) can be
stored in mas[0][j], the values of
f(3, j) in
mas[1][j] and so on.
for (i = 1; i <=
n; i++)
for (j = 1; j <=
m; j++)
if (x[i] ==
y[j])
mas[i%2][j] = 1 +
mas[(i+1)%2][j-1];
else
mas[i%2][j] =
max(mas[(i+1)%2][j],mas[i%2][j-1]);
Print the answer, which
is stored in mas[n][m]. The
first argument is computed modulo 2.
printf("%d\n",mas[n%2][m]);
Algorithm implementation – recursion
#include <stdio.h>
#include <string.h>
#define SIZE 1002
int x[SIZE], y[SIZE],
dp[SIZE][SIZE];
int n, m, i, j, res;
int max(int i, int j)
{
return (i >
j) ? i : j;
}
int lcs(int *x, int *y, int m, int n)
{
if (m == 0
|| n == 0)
return 0;
if (dp[m][n] !=
-1) return dp[m][n];
if (x[m] == y[n])
return dp[m][n] = 1
+ lcs(x, y, m - 1,
n - 1);
else
return dp[m][n] =
max(lcs(x, y, m, n -
1), lcs(x, y, m - 1,
n));
}
int main(void)
{
scanf("%d",
&n);
for (i =
1; i <= n; i++) scanf("%d", &x[i]);
scanf("%d",
&m);
for (i =
1; i <= m; i++) scanf("%d", &y[i]);
memset(dp,
-1, sizeof(dp));
res =
lcs(x, y, n, m);
printf("%d\n",
res);
return 0;
}
Java implementation
import java.util.*;
public class Main
{
static int x[], y[], dp[][];
static int n, m;
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
x = new int[n+1];
for
(int i = 1;
i <= n; i++)
x[i] = con.nextInt();
m = con.nextInt();
y = new int[m+1];
for
(int i = 1;
i <= m; i++)
y[i] = con.nextInt();
dp = new int[2][m+1];
for
(int i = 1;
i <= n; i++)
for
(int j = 1;
j <= m; j++)
if (x[i] == y[j])
dp[i%2][j] = 1
+ dp[(i-1)%2][j-1];
else
dp[i%2][j] =
Math.max(dp[(i-1)%2][j],dp[i%2][j-1]);
System.out.println(dp[n%2][m]);
con.close();
}
}
Java implementation – recursion
import java.util.*;
public class Main
{
static int x[], y[], dp[][];
static int n, m;
public static int lcs(int m, int n)
{
if (m == 0
|| n == 0)
return 0;
if (dp[m][n] !=
-1) return dp[m][n];
if (x[m] == y[n])
return dp[m][n] = 1
+ lcs(m - 1, n - 1);
else
return dp[m][n] =
Math.max(lcs(m, n -
1), lcs(m - 1, n));
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
x = new int[n+1];
for
(int i = 1;
i <= n; i++)
x[i] = con.nextInt();
m = con.nextInt();
y = new int[m+1];
for
(int i = 1;
i <= m; i++)
y[i] = con.nextInt();
dp = new int[n+1][m+1];
for
(int i = 0;
i <= n; i++)
Arrays.fill(dp[i],
-1);
int res = lcs(n,m);
System.out.println(res);
con.close();
}
}
Python implementation
Read the input sequences
into lists x and y.
n = int(input())
x =
[0] + list(map(int, input().split()))
m = int(input())
y =
[0] + list(map(int, input().split()))
Initialize the list dp,
which contains the last two rows of the dynamic transformation.
dp = [[0] * (m + 1) for _ in range(2)]
Compute the values of f(i, j) (1 ≤ i ≤ n,
1 ≤ j ≤ m). Store the results of f(i, j) in the cells dp[i % 2][j].
for i in range(1, n
+ 1):
for j in range(1, m
+ 1):
if x[i] == y[j]:
dp [i
% 2][j] = dp[(i
- 1) % 2][j
- 1] + 1
else:
dp[i %
2][j] = max(dp[(i
- 1) % 2][j],
dp[i % 2][j - 1])
Print the result, which is located in the cell dp[n][m]. The first
argument is computed modulo 2.
print(dp[n %
2][m])