1619. Сбор призов

В видеоигре n призовых коробок расположены в ряд. В каждой коробке находится некоторое количество очков. По правилам игры нельзя выбирать соседние коробки – если будут открыты две соседние коробки, сработает система тревоги, и вы потеряете все призы.

Зная количество очков в каждой коробке, определите максимальное число очков, которое можно собрать, не вызвав тревогу.

Вход. Первая строка содержит количество коробок n (1 ≤ n ≤ 10⁶). Вторая строка содержит n целых неотрицательных чисел a₁, a₂, ..., a_n, где a_i – количество  очков, которое можно получить из i-й коробки.

Выход. Выведите максимальное количество очков, которое можно собрать без срабатывания тревоги.

Пример входа	Пример выхода
5 6 1 2 10 4	16

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Перенумеруем коробки, начиная с первой (i-ая коробка содержит a_i очков). Пусть f(i) обозначает максимальную сумму очков, которую можно получить, рассматривая коробки с 1 по i-ую включительно.

Тогда:

· f(1) = a₁,

· f(2) = max(a₁, a₂)

При вычислении f(i) рассмотрим два случая:

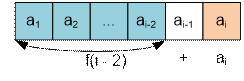
· если выбирается i-я коробка, то соседняя (i – 1)-ая коробка недоступна. В этом случае максимальная сумма очков будет равна f(i – 2) + a_i.

· если i-я коробка не выбирается, то максимальная сумма очков равна f(i – 1).

Таким образом

f(i) = max(f(i – 2) + a_i, f(i – 1))

Запомним значения f(i) в массиве res. Ответом задачи будет значение f(n) = res[n].

Пример

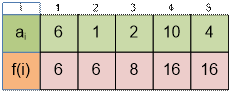
Рассмотрим вычисление f(3)

Если третью коробку не открывать, то мы просто получим лучший результат для первых двух коробок: f(2) = 6.

Если третью коробку открыть, то вторую открыть уже нельзя (они соседние). Значит можно взять оптимальный результат для первой коробки и прибавить очки из третьей:

f(1) + a₃ = 6 + 2 = 8

Выбираем максимум из двух вариантов:

f(3) = max(f(2), f(1) + a₃) = max(6, 8) = 8

Рассмотрим вычисление f(4)

Если четвёртую коробку не открывать, то результат равен f(3) = 8.

Если четвёртую коробку открыть, то третью открывать нельзя. Значит берём лучший результат для первых двух коробок и прибавляем очки из четвёртой:

f(2) + a₄ = 6 + 10 = 16

Выбираем максимум из двух вариантов:

f(4) = max(f(3), f(2) + a₄) = max(8, 16) = 16

Упражнение

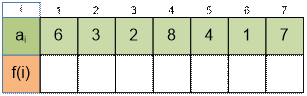
Вычислите значения f(i) для следующих входных данных:

Реализация алгоритма

Объявим входной массив а и результирующий res.

#define MAX 1000001

long long a[MAX], res[MAX];

Читаем входные данные.

scanf("%d",&n);

for (i = 1; i <= n; i++)

scanf("%lld",&a[i]);

Вычисляем ответ для одной res₁ и двух res₂ коробок.

res[1] = a[1];

if (n > 1) res[2] = max(a[1],a[2]);

Вычисляем ответы для остальных коробок.

for (i = 3; i <= n; i++)

res[i] = max(res[i - 2] + a[i], res[i - 1]);

Выводим ответ.

printf("%lld\n",res[n]);

Java реализация

import java.util.*;

class Main

{

static long a[] = new long[1000001];

static long res[] = new long[1000001];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

for (int i = 1; i <= n; i++)

a[i] = con.nextInt();

res[1] = a[1];

if (n > 1) res[2] = Math.max(a[1],a[2]);

for (int i = 3; i <= n; i++)

res[i] = Math.max(res[i - 2] + a[i], res[i - 1]);

System.out.println(res[n]);

con.close();

}

}

Python реализация

Читаем входные данные.

n = int(input())

lst = list(map(int,input().split()))

Инициализируем список dp.

dp = [0] * len(lst)

Вычисляем ответ для одной dp₀ и двух dp₁ коробок.

dp[0] = lst[0]

if (n > 1): dp[1] = max(lst[0], lst[1])

Вычисляем ответы для остальных коробок.

for i in range(2, len(lst)):

dp[i] = max(dp[i-1], dp[i-2] + lst[i])

Выводим ответ.

print(dp[-1])