1619. House Robber

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed away. The only constraint stopping you from robbing each of them is that adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses are broken into on the same night.

Given a list of non-negative integers representing the amount of money in each house, determine the maximum amount of money you can rob tonight without alerting the police.

Input. The first line contains the number of houses n (1 ≤ n ≤ 10⁶). The second line contains n non-negative integers a₁, a₂, ..., a_n, where a_i is the amount of money that can be taken from the i-th house.

Output. Print the maximum sum you can steal tonight without triggering a police alert.

Sample input	Sample output
5 6 1 2 10 4	16

SOLUTION

dynamic programming

Algorithm analysis

Let’s number the houses starting from the first index (the i-th house contains a_i money). Let f(i) be the maximum amount of loot after robbing houses from 1 to the i-th.

Then f(1) = a₁, f(2) = max(a₁, a₂).

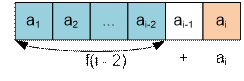
When computing f(i), consider two cases:

· If the i-th house is robbed, then the (i – 1)-th house cannot be robbed. In this case, the profit will be f(i – 2) + a_i.

· if the i-th house is not robbed, the profit will be f(i – 1).

Thus,

f(i) = max(f(i – 2) + a_i, f(i – 1))

Let’s store the values of f(i) in the array res. The answer to the problem will be the value f(n) = res[n].

Example

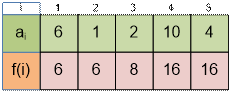
Let’s consider the computation of f(3). If we don’t rob the 3-rd house, the profit will be f(2) = 6. If the 3-rd house is robbed, we can rob the first house, gaining a profit of f(1) = 6, plus the profit from robbing the 3-rd house, which is 2 (the total profit will be 6 + 2 = 8).

Now, let’s consider the computation of f(4). If we don’t rob the 4-th house, the profit will be f(3) = 8. If the 4-th house is robbed, we can rob the first two houses, gaining a profit of f(2) = 6, plus the profit from robbing the 4-th house, which is 10 (the total profit will be 6 + 10 = 16).

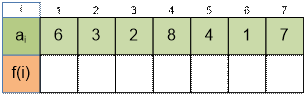
Exercise

Compute the values of f(i) for the following input data:

Algorithm realization

Declare the input array а and the resulting array res.

#define MAX 1000001

long long a[MAX], res[MAX];

Read the input data.

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%lld",&a[i]);

Compute the answer res₁ for one house, and res₂ for two houses.

res[1] = a[1];

if (n > 1) res[2] = max(a[1],a[2]);

Compute the answers for the remaining houses.

for(i = 3; i <= n; i++)

res[i] = max(res[i - 2] + a[i], res[i - 1]);

Print the answer.

printf("%lld\n",res[n]);

Java realization

import java.util.*;

class Main

{

static long a[] = new long[1000001];

static long res[] = new long[1000001];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

for(int i = 1; i <= n; i++)

a[i] = con.nextInt();

res[1] = a[1];

if (n > 1) res[2] = Math.max(a[1],a[2]);

for(int i = 3; i <= n; i++)

res[i] = Math.max(res[i - 2] + a[i], res[i - 1]);

System.out.println(res[n]);

con.close();

}

}

Python realization

Read the input data.

n = int(input())

lst = list(map(int,input().split()))

Initialize the list dp.

dp = [0] * len(lst)

Compute the answer dp₀ for one house, and dp₁ for two houses.

dp[0] = lst[0]

if (n > 1): dp[1] = max(lst[0], lst[1])

Compute the answers for the remaining houses.

for i in range(2, len(lst)):

dp[i] = max(dp[i-1], dp[i-2] + lst[i])

Print the answer.

print(dp[-1])