1704. Умная черепашка

Задано клетчатое поле размером m × n. В левом нижнем углу находится черепашка, которая может двигаться только вправо или вверх. Перед тем как достичь правого верхнего угла, черепашка задалась вопросом: сколько существует различных способов добраться из исходной точки до правого верхнего угла?

Черепашка хоть и умная, но самостоятельно посчитать столь большое количество вариантов пока не может. Помогите черепашке найти ответ на свой вопрос.

Вход. Два натуральных числа m и n, не превышающие 30.

Выход. Выведите количество способов, которыми черепашка сможет добраться из левого нижнего угла в правый верхний.

Пример входа	Пример выхода
4 3	10

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Рассмотрим двумерный массив dp, где dp[i][j] представляет количество способов, которыми черепашка может добраться из клетки (1, 1) до клетки (i, j). Установим dp[1][1] = 1.

Черепашка может попасть в ячейку (i, j) либо из ячейки (i – 1, j), либо из ячейки (i, j – 1). Таким образом, справедливо равенство:

dp[i][j] = dp[i – 1][j] + dp[i][j – 1]

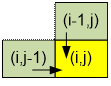
Изначально обнулим массив dp. Особое внимание уделяем обнулению нулевой строки и нулевого столбца массива dp.

· Если i = 1, то dp[i – 1][j] = dp[0][j] = 0 и тогда уравнение динамики упрощается до dp[1][j] = dp[1][j – 1]. Так пересчитывается первая строка.

· Если j = 1, то формула принимает вид dp[i][1] = dp[i – 1][1]. Так пересчитывается первый столбец.

Учитывая, что dp[1][1] = 1, можно заключить, что все ячейки в первой строке и первом столбце будут содержать значение 1, что соответствует единственному способу добраться до каждой из этих ячеек.

Пример

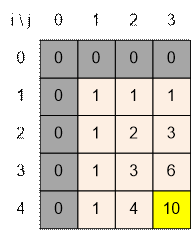
Заполним массив dp для поля размером 4 * 3:

Реализация алгоритма

Объявим рабочий массив dp.

#define MAX 31

long long dp[MAX][MAX];

Читаем входные данные.

scanf("%d %d",&m,&n);

Инициализируем массив dp нулями. Во все ячейки первой строки и первого столбца заносим 1.

memset(dp,0,sizeof(dp));

for(i = 1; i <= m; i++) dp[i][1] = 1;

for(j = 1; j <= n; j++) dp[1][j] = 1;

Пересчитываем значения ячеек массива dp, начиная со второй строки и второго столбца.

for(i = 2; i <= m; i++)

for(j = 2; j <= n; j++)

dp[i][j] = dp[i-1][j] + dp[i][j-1];

Выводим ответ.

printf("%lld\n",dp[m][n]);

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int m = con.nextInt();

int n = con.nextInt();

long dp[][] = new long [m+1][n+1];

for(int i = 1; i <= m; i++) dp[i][1] = 1;

for(int j = 1; j <= n; j++) dp[1][j] = 1;

for(int i = 2; i <= m; i++)

for(int j = 2; j <= n; j++)

dp[i][j] = dp[i-1][j] + dp[i][j-1];

System.out.println(dp[m][n]);

con.close();

}

}

Python реализация

Читаем входные данные.

m, n = map(int,input().split())

Объявим список dp.

dp = [[0] * (n + 1) for i in range(m + 1)]

Во все ячейки первой строки и первого столбца заносим 1.

for i in range(1, m + 1): dp[i][1] = 1

for j in range(1, n + 1): dp[1][j] = 1

Пересчитываем значения ячеек массива dp, начиная со второй строки и второго столбца.

for i in range(2, m + 1):

for j in range(2, n + 1):

dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

Выводим ответ.

print(dp[m][n])