1704. Clever turtle

A grid of size m × n is given. A turtle is located in the bottom left corner and can only move right or up. Before reaching the top right corner, the turtle wondered: how many different ways are there to get from the starting point to the top right corner?

Although the turtle is smart, it is not yet able to calculate such a large number of possibilities on its own. Help the turtle find the answer to its question.

Input. Two positive integers m and n not exceeding 30.

Output. Print the number of ways the turtle can reach the top right corner from the bottom left corner.

Sample input	Sample output
4 3	10

SOLUTION

dynamic programming

Algorithm analysis

Consider a two dimensional array dp, where dp[i][j] represents the number of ways the turtle can get from cell (1, 1) to cell (i, j). We set dp[1][1] = 1.

The turtle can reach cell (i, j) either from cell (i – 1, j) or from cell (i, j – 1). Therefore, the following equality holds:

dp[i][j] = dp[i – 1][j] + dp[i][j – 1]

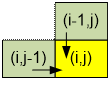
Initially, we’ll zero out the dp array. Special attention is paid to zeroing the first row and first column of the dp array.

· If i = 1, then dp[i – 1][j] = dp[0][j] = 0, and the dynamic programming equation simplifies to dp[1][j] = dp[1][j – 1]. This is how the first row is recalculated.

· If j = 1, the formula becomes dp[i][1] = dp[i – 1][1]. This is how the first column is recalculated.

Given that dp[1][1] = 1, we can conclude that all cells in the first row and the first column will contain the value 1, which corresponds to the only way to reach each of these cells.

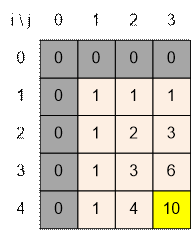
Example

Fill the dp array for the grid of size 4 * 3:

Algorithm realization

Declare the dp array.

long long dp[35][35];

Read the input data.

scanf("%d %d",&m,&n);

Initialize the dp array with zeroes. Set all cells in the first row and first column to 1.

memset(dp,0,sizeof(dp));

for(i = 1; i <= m; i++) dp[i][1] = 1;

for(j = 1; j <= n; j++) dp[1][j] = 1;

Recalculate the values of the dp array cells, starting from the second row and the second column.

for(i = 2; i <= m; i++)

for(j = 2; j <= n; j++)

dp[i][j] = dp[i-1][j] + dp[i][j-1];

Print the answer.

printf("%lld\n",dp[m][n]);

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int m = con.nextInt();

int n = con.nextInt();

long dp[][] = new long [m+1][n+1];

for(int i = 1; i <= m; i++) dp[i][1] = 1;

for(int j = 1; j <= n; j++) dp[1][j] = 1;

for(int i = 2; i <= m; i++)

for(int j = 2; j <= n; j++)

dp[i][j] = dp[i-1][j] + dp[i][j-1];

System.out.println(dp[m][n]);

con.close();

}

Python realization

Read the input data.

m, n = map(int,input().split())

Declare the dp list.

dp = [[0] * (n + 1) for i in range(m + 1)]

Set all cells in the first row and first column to 1.

for i in range(1, m + 1): dp[i][1] = 1

for j in range(1, n + 1): dp[1][j] = 1

Recalculate the values of the dp list cells, starting from the second row and the second column.