1738. Замощение доминошками
Дано игровое
поле размерами n * m, некоторые клетки которого уже замощены. Замостить свободные
соседние клетки поля доминошкой размерами 1 * 2 стоит a условных единиц. Замостить свободную клетку
поля квадратиком размерами 1 * 1 стоит b условных единиц.
Определите,
какая минимальная сумма денег нужна, чтобы дозамостить всё поле.
Вход. Первая строка содержит четыре числа n, m, a, b
(1 ≤ n, m ≤ 100, a, b – целые числа, по модулю не
превосходящие 1000). Каждая из последующих n
строк содержит по m символов: символ “.” (точка)
обозначает занятую клетку поля, а символ “*” (звёздочка) – свободную.
Выход. Выведите
минимальную сумму денег, имея которую можно замостить свободные клетки поля (и
только их).
|
Пример
входа 1 |
Пример
выхода 1 |
|
2 3 3
2 .** .*. |
5 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
3 4 5 3 *..* **** ***. |
23 |
РЕШЕНИЕ
графы –
максимальный поток
Анализ алгоритма
Если два
соседних поля дешевле замостить двумя квадратиками (2*b ≤ a), то ответ
равен b * empty, где empty –
количество свободных клеток.
Построим граф,
количество вершин которого равно числу ячеек доски. Перенумеруем ячейки слева
направо, сверху вниз. Ячейке (i, j) поставим в
соответствие вершину i * m + j графа. Таким образом вершины графа
нумеруются с 0 до m * n –
1. Соединим ребрами все пары соседних пустых ячеек. Далее
раскрасим вершины графа в шахматном порядке двумя цветами. Вершины, окрашенные
серым, отнесем к первой доле, а белым – ко второй. Таким образом построенный
граф оказался двудольным. Найдем величину максимального паросочетания в нем.
Оно равно максимальному количеству костей домино, которое можно положить на
пустые клетки доски.
Если удвоенная
величина максимального паросочетания не равна количеству пустых клеток, то
остальные пустые клетки следует заполнять единичными квадратиками.
Пример
Рассмотрим второй тест. Пронумеруем вершины графа. Вершину (i, j) считаем серой, если сумма i
+ j четна. Проведем ребра из серых
вершин в соседние пустые.
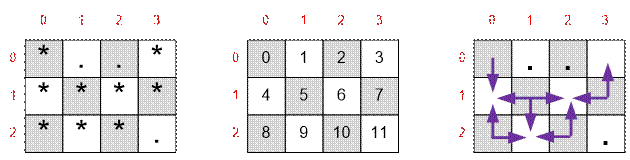
Двудольный граф
примет следующий вид. Максимальное паросочетание равно 4. Его образуют ребра 0 → 4, 5 → 6, 7
→ 3, 8 → 9.
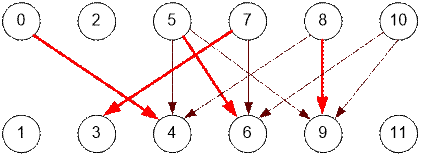
Этому
паросочетанию соответствует следующая укладка костей домино 1 * 2. Одна клетка
остается непокрытой, ее следует замостить квадратиком размерами 1 * 1.
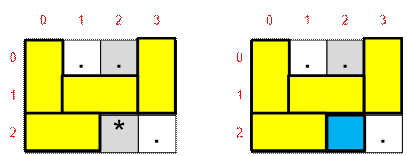
Входное поле мы
замостили 4 домино размером 1 * 2 и 1 квадратом размером 1 * 1. Стоимость
покрытия составляет 5 * 4 + 3 = 23.
Реализация алгоритма
Доску будем хранить в массиве строк s. Граф строим в
массиве g.
#define MAX 110
string s[MAX];
vector<vector<int> > g;
vector<int> mt, used;
Ищем дополняющую цепь из вершины v поиском в глубину.
int dfs(int
v)
{
if (used[v]) return 0;
used[v] = 1;
for (int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
if (mt[to]
== -1 || dfs(mt[to]))
{
mt[to] = v;
return 1;
}
}
return 0;
}
Основная часть
программы. Читаем входные данные.
cin >> n >> m >> a >> b;
for (i = 0; i < n; i++)
cin >> s[i];
Строим граф g. Количество его вершин
равно n * m, вершины нумеруются с нуля. Для
каждой серой вершины, которой соответствует пустая клетка доски, строим список
смежных с ней вершин. Вершину, соответствующую ячейке (i, j), будем считать
серой, если сумма i + j четна.
g.resize(n*m);
empt = 0;
for(i = 0; i < n; i++)
for(j = 0; j < m; j++)
{
if (s[i][j]
== '.') continue;
empty++;
if ((i + j) %
2) continue;
Ячейка (i, j) серая и пустая. Она
соответствует вершине i * m + j графа. Для каждой соседней с ней пустой ячейки проводим в нее
ориентированное ребро. Соседние с (i,
j) ячейки перебираем в порядке:
левая, правая, верхняя, нижняя.
int u = i * m + j;
if ((j > 0)
&& (s[i][j - 1] == '*')) g[u].push_back(u
- 1);
if ((j < m - 1)
&& (s[i][j + 1] == '*')) g[u].push_back(u
+ 1);
if ((i > 0)
&& (s[i - 1][j] == '*')) g[u].push_back(u
- m);
if ((i < n - 1)
&& (s[i + 1][j] == '*')) g[u].push_back(u
+ m);
}
Если 2 * b ≤ a, то дешевле свободные клетки замощать
единичными квадратиками.
if (2 * b <= a)
{
cout << empt * b << endl;
return 0;
}
Ищем дополняющий путь из каждой серой
вершины, запуская из нее поиск в глубину.
mt.assign(n*m,
-1);
for(i = 0; i < n; i++)
for(j = 0; j < m; j++)
{
if ((i + j) %
2) continue;
used.assign(n*m, 0);
dfs(i * m + j);
}
Вычисляем величину максимального
паросочетания в переменной c. Оно
равно количеству покрывающих доминошек 1 * 2.
c = 0;
for (i = 0; i < n * m; i++)
if (mt[i] !=
-1) c++;
Вычисляем стоимость res покрытия свободных клеток поля и
выводим ее.
res = c * a +
(empty - 2*c) * b;
cout << res << endl;
Реализация с оптимизацией
#include <iostream>
#include <vector>
#include <string>
#define MAX 102
using namespace std;
string s[MAX];
int empt, res, n, m, a, b, i, j, c;
vector<vector<int> > g;
vector<int> mt, used, par;
int dfs(int v)
{
if (used[v]) return 0;
used[v] = 1;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if (mt[to] == -1 || dfs(mt[to]))
{
mt[to] = v;
par[v] = to;
return 1;
}
}
return 0;
}
void AugmentingPath(void)
{
int i, j, run;
mt.assign(n * m, -1);
par.assign(n * m, -1);
Начальной жадной инициализации нет
смысла проводить, так как она фактически происходит на первой итерации цикла
for.
for (run = 1; run; )
{
run = 0; used.assign(n * m, 0);
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
{
if ((i + j) % 2) continue;
if ((par[i * m + j] == -1) && dfs(i * m + j))
run = 1;
}
}
}
int main(void)
{
cin >> n >> m >> a >> b;
for (i = 0; i < n; i++)
cin >> s[i];
g.resize(n * m); empt = 0;
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
{
if (s[i][j] == '.') continue;
empt++;
if ((i + j) % 2) continue;
int u = i * m + j;
if ((j > 0) &&
(s[i][j - 1] == '*'))
g[u].push_back(u - 1); // left
if ((j < m - 1) && (s[i][j + 1] == '*'))
g[u].push_back(u + 1); // right
if ((i > 0) &&
(s[i - 1][j] == '*'))
g[u].push_back(u - m); // up
if ((i < n - 1)
&& (s[i + 1][j] == '*'))
g[u].push_back(u + m); // down
}
if (2 * b <= a)
{
cout << empt * b << endl;
return 0;
}
AugmentingPath();
c = 0;
for (i = 0; i < n * m;
i++)
if (mt[i] != -1) c++;
res = c * a + (empt - 2 * c) * b;
cout << res << endl;
return 0;
}