1781. Задача о назначениях
Одной из классических задач
комбинаторной оптимизации является так называемая “задача о назначениях”. Формулируется она следующим образом.
Есть n работников, пронумерованных числами от 1 до n, и n работ, также пронумерованных числами от
1 до n. Если i-ый работник выполняет j-ую работу,
то ему выплачивается зарплата в размере cij денежных
единиц. Необходимо найти такое назначение работников на работы (каждый работник
выполняет ровно одну работу, каждая работа выполняется ровно одним работником),
что суммарная зарплата работников минимальна (соответствующая сумма называется стоимостью
назначения).
Напишите программу, решающую
задачу о назначениях.
Вход. Первая строка содержит целое число n (1 ≤
n ≤ 10).
Каждая из следующих n строк
содержит n чисел. При этом j-ое число (i + 1) -ой строки
равно cij (1 ≤ cij ≤ 1000).
Выход. Выведите минимальную возможную
стоимость назначения.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 5 2 3 4 2 1 3 7 6 |
6 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
21 2 3 4 |
5 |
РЕШЕНИЕ
перебор
Анализ алгоритма
Поскольку n ≤ 10, задачу можно решить перебором.
При помощи
функции next_permutation сгенерируем все возможные перестановки работников. То есть рассмотрим все возможные
назначения n работников на n работ. Для каждого возможного назначения найдем стоимость
выполнения работ. Среди всех найденных стоимостей найдем наименьшую.
Пример
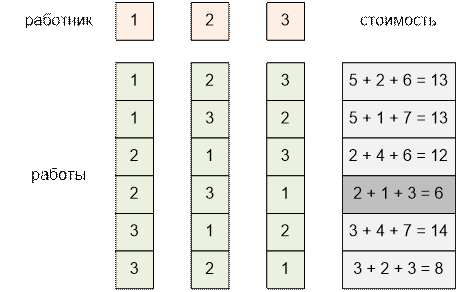
Рассмотрим в первом
примере все возможные назначения трех работников на три работы.
Реализация алгоритма
Матрицу зарплат храним в массиве cost. В массиве m генерируем все
возможные перестановки чисел от 0 до n – 1. Для удобства
перенумеруем работников от 0 до n – 1.
int m[11], cost[11][11];
Читаем входные данные.
scanf("%d", &n);
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
scanf("%d", &cost[i][j]);
В массив m заносим наименьшую перестановку – числа от 0 до n – 1.
for (i = 0; i < n; i++) m[i] = i;
Минимальную стоимость назначения
будем вычислять в переменной res.
res = 2000000000;
Генерируем
все возможные перестановки в массиве m.
do
{
Для
текущей перестановки в переменной sum находим стоимость выполнения
работ. Работник номер i выполняет работу номер m[i] стоимостью cost[i][m[i]].
int sum = 0;
for (i = 0; i < n; i++) sum += cost[i][m[i]];
Среди
всех вычисленных стоимостей находим наименьшую.
res = min(res, sum);
} while (next_permutation(m, m + n));
Выводим ответ.
printf("%d\n", res);