1788. Обратная перестановка
По заданной
перестановке p найдите ей обратную p-1.
Вход. В первой строке записан порядок n (0 < n ≤
20000) перестановки p. Во второй
строке записана сама перестановка p.
Выход. Выведите искомую перестановку p-1.
|
Пример
входа |
Пример
выхода |
|
3 2 3 1 |
3 1 2 |
РЕШЕНИЕ
комбинаторика
- перестановки
Анализ алгоритма
Пусть p – заданная
перестановка. Ее применение означает перенос элемента из позиции i в позицию p[i], то есть происходит преобразование i ® p[i]. Обратной для
p будет такая перестановка pi, для которой имеет место обратное преобразование
p[i] ® i. То есть в
массиве pi на p[i]-ом месте должно стоять
число i (pi[p[i]] = i).
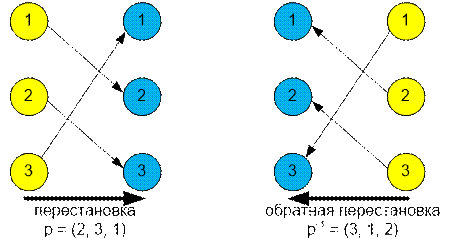
Пример
Изобразим прямую p = ![]() и обратную p-1 =
и обратную p-1 = ![]() перестановки. В
обратной перестановке ребра ориентированы в другую сторону.
перестановки. В
обратной перестановке ребра ориентированы в другую сторону.
Реализация алгоритма
Массив p хранит входную перестановку, массив pi хранит
обратную.
#define MAX 20010
int p[MAX], pi[MAX];
Читаем входную перестановку.
scanf("%d",&n);
for(i = 1; i <= n; i++)
scanf("%d",&p[i]);
Вычисляем обратную перестановку.
for(i = 1; i <= n; i++)
pi[p[i]] = i;
Выводим обратную перестановку.
for(i = 1; i <= n; i++)
printf("%d
",pi[i]);
printf("\n");
Python реализация
Список p
хранит входную перестановку, список pi хранит обратную. Читаем входные
данные.
n = int(input())
p = [0] + list(map(int, input().split()))
pi = [0] * (n + 1)
Вычисляем
обратную перестановку.
for i in range(1, n + 1):
pi[p[i]] = i
Выводим обратную
перестановку.
for i in range(1, n + 1):
print(pi[i], end=" ")
print()