1788. Tərs dəyişdirmə

Verilmiş dəyişdirmə p üçün onun inversini p^-1 tapın.

Giriş. İlk sətirdə dəyişdirmənin sırası n (0 < n ≤ 20000) yazılır. İkinci sətirdə isə özü dəyişdirmə p yazılır.

Çıxış. Axtarılan invers dəyişdirmə p^-1 bir sətirdə çap olunmalıdır.

Nümunə giriş	Nümunə çıxış
3 2 3 1	3 1 2

HƏLLİ

kombinatorika - dəyişdirmələr

Alqoritmin analizi

Əvvəlcədən təyin edilmiş dəyişdirmə kimi p düşünək. Onun tətbiqi i pozisiyadan p[i] pozisiyaya element keçirilməsi deməkdir, başqa bir deyil p[i] pozisiyasından i pozisiyaya keçirilərək əməliyyatı i ® p[i] olur. p üçün əksi dəyişdirmə pi kimi olacaq ki, onun üçün əksi dəyişdirmə pi, əvvəlki dəyişdirmənin əksinə olaraq p[i] ® i keçirilməsi deməkdir. Yəni pi massivində i üçün p[i] pozisiyasında i olmalıdır (pi[p[i]] = i).

Nümunə

Düzənli p = 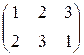və əks p^-1 = 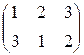dəyişdirmələrini təsvir edək. Əks dəyişdirmədə kenarlar digər istiqamətdə oxlanmışdır.

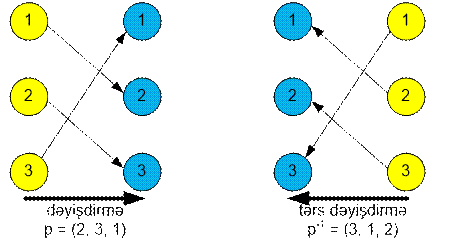
Algoritmin reallaşdırılması

p massivi giriş dəyişdirməsini saxlayır, pi massivi əksini saxlayır.

#define MAX 20010

int p[MAX], pi[MAX];

Giriş dəyişdirməsini oxuyuruq.

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&p[i]);

Əks dəyişdirməni hesablayırıq.

for(i = 1; i <= n; i++)

pi[p[i]] = i;

Əks dəyişdirməni çap edirik.

for(i = 1; i <= n; i++)

printf("%d ",pi[i]);

printf("\n");

Python reallaşdırılması

Siyahı p giriş dəyişdirməsini saxlayır, siyahı pi tərsini saxlayır. Giriş məlumatlarını oxuyuruq.

n = int(input())

p = list(map(int, input().split()))

pi = [0] * (n + 1)

Tərs dəyişdirməni hesablayırıq.

for i in range(1, n + 1):

pi[p[i - 1]] = i

Tərs dəyişdirməni çap edirik.

for i in range(1, n + 1):

print(pi[i], end=" ")

print()