1788. Inverse permutation

Given a permutation p, find its inverse p^-1.

Input. The first line contains the order n (0 < n ≤ 20000) of the permutation p. The second line contains the permutation p.

Output. Print the inverse permutation p^-1.

Sample input	Sample output
3 2 3 1	3 1 2

SOLUTION

combinatorics - permutations

Algorithm analysis

Let p be a given permutation. Its application means moving an element from position i to position p[i], i.e., the transformation i ® p[i] occurs. The inverse permutation of p, denoted as pi, will have the inverse transformation where p[i] ® i takes place. In other words, in the array pi, the number i should be placed at position p[i] (pi[p[i]] = i).

Example

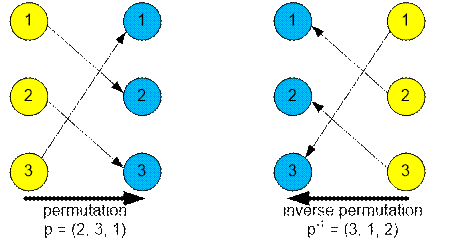
Consider the permutation p = and its inverse p^-1 = . In the inverse permutation the edges are oriented in the opposite direction.

Algorithm realization

The array p stores the input permutation, and the array pi stores the inverse permutation.

#define MAX 20010

int p[MAX], pi[MAX];

Read the input permutation.

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&p[i]);

Compute the inverse permutation.

for(i = 1; i <= n; i++)

pi[p[i]] = i;

Print the inverse permutation.

for(i = 1; i <= n; i++)

printf("%d ",pi[i]);

printf("\n");

Python realization

The list p stores the input permutation, and the list pi stores the inverse permutation. Read the input data.

n = int(input())

p = [0] + list(map(int, input().split()))

pi = [0] * (n + 1)

Compute the inverse permutation.

for i in range(1, n + 1):

pi[p[i]] = i

Print the inverse permutation.

for i in range(1, n + 1):

print(pi[i], end=" ")

print()