1796. Diameter of the graph

The connected weighted and undirected graph is given.

Consider the pair of vertices, for which the distance between them is maximum among all pairs of vertices. Such distance is called the graph diameter. The eccentricity of the vertex v is the maximal distance from the vertex v to all other vertices of the graph. The radius of the graph is minimal eccentricity of the vertices.

Find the diameter and the radius of the graph.

Input. The first line contains the number of graph vertices n (1 ≤ n ≤ 100). Each of the next n lines contains n numbers – the adjacency matrix of the graph, where -1 means the absence of the edge between the vertices, and any nonnegative integer means the edge with the given weight. The main diagonal of the matrix contains zeros; the edge weights do not exceed 1000.

Output. Print two numbers: the diameter and the radius of the graph.

Sample input	Sample output
4 0 -1 1 2 -1 0 -1 5 1 -1 0 4 2 5 4 0	8 5

SOLUTION

graphs – Floyd - Warshall

Algorithm analysis

Using the Floyd – Warshall algorithm, construct a matrix of shortest distances between the graph vertices. Denote by v₁, v₂, …, v_n the vertices of the graph, by d(v_i, v_j) the shortest distance between the vertices v_i and v_j. Compute

r(v_i) =

Then the minimum value among r(v_i) is the radius of the graph, and the maximum is the diameter.

Example

Graph given in a sample, has a form:

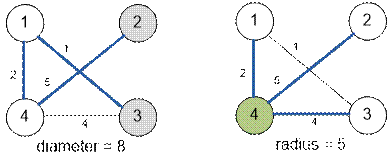
The largest distance between pairs of vertices (2 and 3) is 8 (graph diameter). The smallest distance is the maximum distance from vertex 4 to other vertices of the graph and equals to 5 (graph radius).

Algorithm realization

Declare the constants and the weight matrix of the graph.

#define MAX 110

#define INF 0x3F3F3F3F

int g[MAX][MAX];

Function floyd implements the Floyd – Warshall algorithm.

void floyd(void)

{

int i, j, k;

for(k = 0; k < n; k++)

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

if (g[i][k] + g[k][j] < g[i][j])

g[i][j] = g[i][k] + g[k][j];

}

The main part of the program. Read the input data.

scanf("%d",&n);

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

{

scanf("%d",&g[i][j]);

if (g[i][j] < 0) g[i][j] = INF;

}

Run the algorithm that finds the shortest distances in the graph.

floyd();

For each i-th vertex, find the maximum distance max from it to other vertices. Among all such maximums, find a minimum that equals to the graph radius. The maximum of the maxima equals to the diameter of the graph.

diam = 0; radius = INF;

for(i = 0; i < n; i++)

{

max = 0;

for(j = 0; j < n; j++)

if (g[i][j] > max) max = g[i][j];

if (max > diam) diam = max;

if (max < radius) radius = max;

}

Print the diameter and radius of the graph.

printf("%d\n%d\n",diam,radius);

Java realization

import java.util.Scanner;

public class Main

{

static final int INF = 0x3F3F3F3F;

static int g[][];

static int n;

static void floyd()

{

for(int k = 0; k < n; k++)

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

if (g[i][k] + g[k][j] < g[i][j])

g[i][j] = g[i][k] + g[k][j];

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

g = new int[n][n];

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

{

g[i][j] = con.nextInt();

if (g[i][j] < 0) g[i][j] = INF;

}

floyd();

int diam = 0, radius = INF;

for(int i = 0; i < n; i++)

{

int max = 0;

for(int j = 0; j < n; j++)

if (g[i][j] > max) max = g[i][j];

if (max > diam) diam = max;

if (max < radius) radius = max;

}

System.out.println(diam + "\n" + radius);

con.close();

}

}