1868. Функция
Вычислите
функцию:
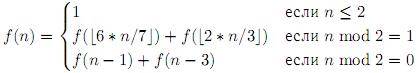
Вход. Одно натуральное число n (1 ≤ n ≤ 1012).
Выход. Выведите значение
f(n), взятое по модулю 232.
|
Пример
входа |
Пример
выхода |
|
7 |
10 |
РЕШЕНИЕ
структуры данных – map,
рекурсия
Анализ алгоритма
Для запоминания
результатов значений функции f из-за
ограничения n ≤ 1012
невозможно использовать линейный массив. С этой целью будем использовать
структуру данных map.
Остается
написать рекурсивную реализацию функции f, запоминая промежуточные результаты.
Реализация алгоритма
Объявим
отображение m. Реализуем вычисление функции f. Поскольку m[n] имеет тип unsigned int, то все суммирования в
функции f будут выполняться по модулю 232, как того
требуется в условии задачи.
map<unsigned long long, unsigned int> m;
unsigned int
f(unsigned long
long n)
{
Если значение f(n) еще не посчитано
и соответственно значение m[n] еще не
присвоено, то по умолчанию считается m[n] = 0. Если m[n] > 0, то f(n) уже вычислено и
хранится в m[n]. Нет смысла считать его еще раз, просто
возвращаем m[n].
if (m[n] >
0) return m[n];
Базовый случай.
if (n <=
2) return m[n] = 1;
В зависимости от четности n вычисляем f(n).
if (n &
1)
return m[n]
= f(6*n/7) + f(2*n/3);
else
return m[n]
= f(n - 1) + f(n - 3);
}
Основная часть программы. Читаем значение n и выводим f(n).
scanf("%llu",&n);
printf("%u\n",f(n));
Java реализация
import java.util.*;
public class Main
{
static
Map<Long, Long> m = new
HashMap<Long, Long>();
static long MOD
= (long) Math.pow(2, 32);
public static long f(long n)
{
if
(m.containsKey(n)) return m.get(n);
if (n
<= 2)
{
m.put(n, (long)1);
return 1;
}
long res;
if (n %
2 == 1)
res = (f(6*n/7) +
f(2*n/3)) % MOD;
else
res = (f(n-1) +
f(n-3)) % MOD;
m.put(n,res);
return
res;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
long n =
con.nextLong();
System.out.println(f(n));
con.close();
}
}