1868. Function
Calculate the function:
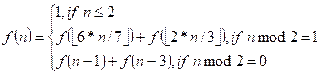
Input. One positive integer n (1 ≤ n
≤ 1012).
Output. Print the value of f(n) modulo 232.
|
Sample
input |
Sample
output |
|
7 |
10 |
SOLUTION
data
structures –
map, recursion
Algorithm analysis
Because of the
limitation n ≤ 1012, it is impossible to use a linear
array to store the results of the values of the function f. For this purpose,
we’ll use the map data structure.
It remains to
write a recursive implementation of the function f, memoizing the
intermediate results.
Algorithm realization
Declare the map m. Implement the computation of the function
f. Since m[n] is of unsigned int type, all summations in
the f function will be performed modulo 232, as required in the problem statement.
map<unsigned long long, unsigned int> m;
unsigned int
f(unsigned long
long n)
{
If the value f(n)
has not yet been calculated and, accordingly, the value m[n] has not yet been assigned, then its default value is m[n] = 0. If m[n] > 0, then f(n) has already been calculated and stored
in m[n]. It makes no sense to compute it again, just
return m[n].
if (m[n] >
0) return m[n];
The base case.
if (n <=
2) return m[n] = 1;
Compute f(n) depending on the parity of n.
if (n &
1)
return m[n]
= f(6*n/7) + f(2*n/3);
else
return m[n]
= f(n - 1) + f(n - 3);
}
The main part of the program. Read the value of n and print f(n).
scanf("%llu",&n);
printf("%u\n",f(n));
Java realization
import java.util.*;
public class Main
{
static
Map<Long, Long> m = new
HashMap<Long, Long>();
static long MOD
= (long) Math.pow(2, 32);
public static long f(long n)
{
if
(m.containsKey(n)) return m.get(n);
if (n
<= 2)
{
m.put(n, (long)1);
return 1;
}
long res;
if (n %
2 == 1)
res = (f(6*n/7) +
f(2*n/3)) % MOD;
else
res = (f(n-1) +
f(n-3)) % MOD;
m.put(n,res);
return
res;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
long n =
con.nextLong();
System.out.println(f(n));
con.close();
}
}