115. Две цифры

Сколько можно составить n-значных чисел, используя цифры 5 и 9, в которых три одинаковые цифры не стоят рядом?

Вход. Одно число n (n ≤ 30).

Выход. Выведите количество n-значных чисел.

Пример входа	Пример выхода
3	6

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Искомых однозначных чисел всего два: 5 и 9.

Искомых двузначных чисел четыре: 55, 59, 95 и 99.

Искомые n-значные числа будем строить следующим образом. Возьмем все построенные (n – 1)-значные числа и припишем к ним цифру, которая не совпадает с их последней. Таким образом получим n-значные числа, которые заканчиваются на 559, 595, 959 и 995.

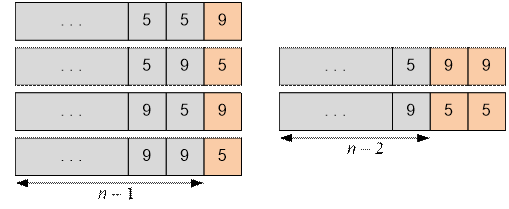
К n-значным числам также отнесем те, которые можно получить из (n – 2)-значных приписыванием двух пятерок или двух девяток так, чтобы не получилось три последних одинаковых цифры. То есть к n-значным числам добавятся те, которые заканчиваются на 599 и 955.

Если через f(n) обозначить количество искомых n-значных чисел, то получим рекуррентность:

f(n) = f(n – 1) + f(n – 2),

f(1) = 2, f(2) = 4

Пример

Искомых двузначных чисел четыре: 55, 59, 95 и 99.

Искомых трехзначных чисел шесть: 559, 595, 959, 995, 599 и 955. Они получаются:

· от двузначных: 55 → 559, 59 → 595, 95 → 959, 99 → 995

· от одназначных: 5 → 599, 9 → 955

Все множество искомых четырехзначных чисел получим из:

· трехзначных чисел, приписав к ним цифру, отличную от последней: 5595, 5959, 9595, 9959, 5995 и 9559.

· двузначных чисел, приписав к ним 55 или 99 так чтобы не получить три одинаковые цифры: 5599, 5955, 9599 и 9955.

Реализация алгоритма

Значение f(i) будем хранить в ячейке m[i].

int m[31];

Читаем входное значение n.

scanf("%d", &n);

Заносим значения f(1) = 2 и f(2) = 4 в массив.

m[1] = 2; m[2] = 4;

Вычисляем значения m[i] (3 ≤ i ≤ n) по рекуррентной формуле.

for(i = 3; i <= n; i++)

m[i] = m[i-1] + m[i-2];

Выводим ответ – значение m[n].

printf("%d\n",m[n]);

Java реализация

import java.util.*;

public class Main

{

public static int MAX = 32;

static int m[] = new int[MAX];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

m[1] = 2; m[2] = 4;

for(int i = 3; i <= n; i++) m[i] = m[i-1] + m[i-2];

System.out.println(m[n]);

}

}

Python реализация

Читаем входное значение n.

n = int(input())

Инициализируем список m.

m = [0] * 31

Заносим значения f(1) = 2 и f(2) = 4 в список.

m[1] = 2

m[2] = 4

Вычисляем значения m[i] (3 ≤ i ≤ n) по рекуррентной формуле.

for i in range(3, n + 1):

m[i] = m[i - 1] + m[i - 2]

Выводим ответ – значение m[n].

print(m[n])