115. Two digits

How many n-digit numbers can be created using only digits 5 and 9, where no three identical digits stand side by side?

Input. One number n (n ≤ 30).

Output. The amount of n-digit numbers.

Sample input	Sample output
3	6

SOLUTION

dynamic programming

Algorithm analysis

There are only two desired single-digit numbers: 5 and 9.

There are four desired two-digit numbers: 55, 59, 95 and 99.

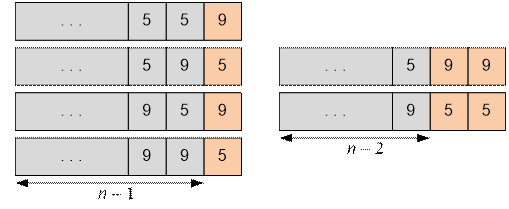
We shall construct the desired n-digit numbers as follows. Take all the constructed (n – 1) - digit numbers and append to them a digit that does not match their last digit. This way, we obtain n-digit numbers ending in 559, 595, 959 and 995.

To the n-digit numbers, we will also include those that can be obtained from (n – 2)-digit numbers by appending two fives or two nines so that three consecutive identical digits are not obtained. That is, to the n-digit numbers, we add those that end in 599 and 955.

If we denote the number of desired n-digit numbers as f(n), then we obtain the recurrence:

f(n) = f(n – 1) + f(n – 2), f(1) = 2, f(2) = 4

Example

There are four two-digit numbers: 55, 59, 95 and 99.

There are six three-digit numbers: 559, 595, 959, 995, 599 and 955.

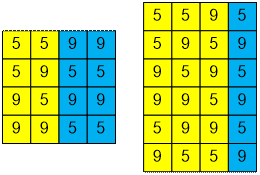
The set of all desired four-digit numbers we can get from:

· three-digit numbers by appending a digit different from the last one: 5595, 5959, 9595, 9959, 5995 and 9559.

· two-digit numbers by appending 55 or 99 to them so as not to obtain three identical digits: 5599, 5955, 9599 and 9955.

Algorithm realization

The value of f(i) will be stored in cell m[i].

int m[31];

Read the input value of n.

scanf("%d", &n);

Store the values f(1) = 2 and f(2) = 4 in the array.

m[1] = 2; m[2] = 4;

Compute the values m[i] (3 ≤ i ≤ n) according to the recurrence formula.

for(i = 3; i <= n; i++)

m[i] = m[i-1] + m[i-2];

Print the answer – the value of m[n].

printf("%d\n",m[n]);

Java realization

import java.util.*;

public class Main

{

public static int MAX = 32;

static int m[] = new int[MAX];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

m[1] = 2; m[2] = 4;

for(int i = 3; i <= n; i++) m[i] = m[i-1] + m[i-2];

System.out.println(m[n]);

}

}

Python realization

Read the input value of n.

n = int(input())

Initialize a list m.

m = [0] * 31

Store the values f(1) = 2 and f(2) = 4 in the list.

m[1] = 2

m[2] = 4

Compute the values m[i] (3 ≤ i ≤ n) according to the recurrence formula.

for i in range(3, n + 1):

m[i] = m[i - 1] + m[i - 2]

Print the answer – the value of m[n].

print(m[n])