122. Горные маршруты

Горный туристический комплекс состоит из n турбаз, соединенных между собой k горными переходами (другие маршруты в горах опасны). Любой переход между двумя базами занимает 1 день. Туристическая группа находится на базе a и собирается попасть на базу b не более чем за d дней. Сколько существует разных таких маршрутов (без циклов) между a и b?

Вход. В первой строке через пробел записаны числа n, k, a, b, d (n ≤ 50, d ≤ 10). Каждая из следующих k строк содержит пару чисел, которая описывает возможный горный переход. Все числовые значения натуральные.

Выход. Вывести одно число – количество маршрутов.

Пример входа	Пример выхода
5 8 2 5 3 1 2 1 3 1 5 2 1 2 4 3 4 3 5 4 1	3

РЕШЕНИЕ

графы – поиск в глубину

Анализ алгоритма

Имеется ориентированный граф, в котором требуется найти количество путей между двумя вершинами. Задачу будем решать полным перебором. Начиная с вершины a, поиском в глубину дойдем до вершины b. Далее при помощи бектрекинга будем перебирать все возможные пути из a в b, подсчитывая их количество в переменной res. Длина всех найденных путей не должна превышать d.

Пример

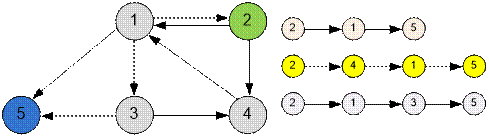
В примере из условия между турбазами 2 и 5 существует 3 ациклических пути длины не больше 3.

Реализация алгоритма

Матрицу смежности графа храним в массиве g.

#define MAX 51

int g[MAX][MAX], used[MAX];

Запускаем поиск в глубину из вершины v. При этом известно, что длина пути от a до v уже равна depth.

void dfs(int v, int depth)

{

if (depth > d) return;

Если мы пришли в вершину b, то найден еще один маршрут. Увеличиваем количество путей res на единицу и возвращаемся назад.

if (v == b)

{

res++;

return;

}

Отмечаем вершину v пройденой.

used[v] = 1;

Ищем вершину i, в которую можно попасть из v.

for(int i = 1; i <= n; i++)

if (g[v][i] && !used[i]) dfs(i,depth+1);

Поскольку происходит перебор вершин с возвратом, то следует установить вершину v как непройденную.

used[v] = 0;

}

Основная часть программы. Читаем входные данные. Ориентированный граф читаем в матрицу смежности g.

scanf("%d %d %d %d %d",&n,&k,&a,&b,&d);

memset(g,0,sizeof(g));

memset(used,0,sizeof(used));

for(i = 0; i < k; i++)

{

scanf("%d %d",&a1,&a2);

g[a1][a2] = 1;

}

Запускаем поиск в глубину из вершины a.

res = 0;

dfs(a,0);

Выводим количество найденных маршрутов.

printf("%d\n",res);

Java реализация

import java.util.*;

public class Main

{

static int g[][], used[];

static int n, k, a, b, d, res;

static void dfs(int v, int depth)

{

if (depth > d) return;

if (v == b)

{

res++;

return;

}

used[v] = 1;

for(int i = 1; i <= n; i++)

if (g[v][i] == 1 && used[i] == 0) dfs(i,depth+1);

used[v] = 0;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

k = con.nextInt();

a = con.nextInt();

b = con.nextInt();

d = con.nextInt();

g = new int[n+1][n+1];

used = new int[n+1];

for(int i = 0; i < k; i++)

{

int a1 = con.nextInt();

int a2 = con.nextInt();

g[a1][a2] = 1;

}

res = 0;

dfs(a,0);

System.out.println(res);

con.close();

}

}