122. Mountain routes

The mountain tourist resort consists of n hostels, connected with k mountain routes (other routes in mountains are dangerous). Any route between two hostels takes 1 day. The travel group, located in the hostel a, is going to go to the hostel b for no more than d days. How many different routes (without cycles) between a and b exist?

Input. The first line contains numbers n, k, a, b, d (n ≤ 50, d ≤ 10), separated by space. Each of the next k lines contains pair of numbers that describes the possible mountain route. All given numbers are positive integers.

Output. Print one number – the number of routes.

Sample input	Sample output
5 8 2 5 3 1 2 1 3 1 5 2 1 2 4 3 4 3 5 4 1	3

SOLUTION

graphs – depth first search

Algorithm analysis

There is a directed graph where you need to find the number of paths between two vertices. We’ll solve the problem by exhaustive search. Starting from the vertex a, using the depth first search strategy, we’ll go to the vertex b. Next, using backtracking, iterate over all possible paths from a to b, counting their number in the variable res. The length of all found paths must not exceed d.

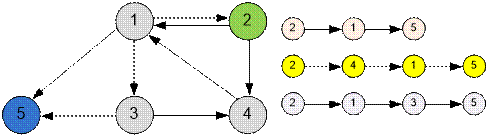
Example

In the sample given between the hostels 2 and 5 there are 3 acyclic paths of length at most 3.

Algorithm realization

Store the adjacency matrix of the graph in the array g.

#define MAX 51

int g[MAX][MAX], used[MAX];

Start the depth first search from the vertex v. It is known that the length of the path from a to v already equals to depth.

void dfs(int v, int depth)

{

if (depth > d) return;

If we come to vertex b, then another route has been found. Increase the number of paths res by one and return back.

if (v == b)

{

res++;

return;

}

Mark the vertex v as visited.

used[v] = 1;

We are looking for a vertex i, where we can go from v.

for(int i = 1; i <= n; i++)

if (g[v][i] && !used[i]) dfs(i,depth+1);

Since the iteration of vertices is performed with backtracking, the vertex v should be set as not visited.

used[v] = 0;

}

The main part of the program. Read the input data. Read the directed graph into the adjacency matrix g.

scanf("%d %d %d %d %d",&n,&k,&a,&b,&d);

memset(g,0,sizeof(g));

memset(used,0,sizeof(used));

for(i = 0; i < k; i++)

{

scanf("%d %d",&a1,&a2);

g[a1][a2] = 1;

}

Run the depth first search from the vertex a.

res = 0;

dfs(a,0);

Print the number of found routes.

printf("%d\n",res);

Java realization

import java.util.*;

public class Main

{

static int g[][], used[];

static int n, k, a, b, d, res;

static void dfs(int v, int depth)

{

if (depth > d) return;

if (v == b)

{

res++;

return;

}

used[v] = 1;

for(int i = 1; i <= n; i++)

if (g[v][i] == 1 && used[i] == 0) dfs(i,depth+1);

used[v] = 0;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

k = con.nextInt();

a = con.nextInt();

b = con.nextInt();

d = con.nextInt();

g = new int[n+1][n+1];

used = new int[n+1];

for(int i = 0; i < k; i++)

{

int a1 = con.nextInt();

int a2 = con.nextInt();

g[a1][a2] = 1;

}

res = 0;

dfs(a,0);

System.out.println(res);

con.close();

}

}